题目内容
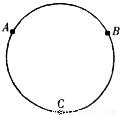
 如图所示的圆环是由阻值90Ω、粗细均匀的金属丝制成的.A、B、C三点将圆环分成三等份,若将其中任意两点连入电压为3V的电路,则通过圆环的总电流为
如图所示的圆环是由阻值90Ω、粗细均匀的金属丝制成的.A、B、C三点将圆环分成三等份,若将其中任意两点连入电压为3V的电路,则通过圆环的总电流为分析:A、B两点间的电阻值可以认为是AB和ACB两段电阻的并联后的总阻值,根据并联电路总电阻的倒数等于各并联电阻的倒数之和即可求出两点间的电阻,最后根据欧姆定律求出通过圆环的电流.
解答: 解:阻值为R的电阻丝弯成一圆环,A、B、C三点将圆环三等分,所以AB段的电阻RADB=
解:阻值为R的电阻丝弯成一圆环,A、B、C三点将圆环三等分,所以AB段的电阻RADB=
R,ACB段的电阻RACB=
R,
∵两段导体并联,
∴
=
+
,
即:
=
+
,
解得:R并=
R=
×90Ω=20Ω;
则通过圆环的总电:I=
=
=0.15A.
故答案为:0.15.
 解:阻值为R的电阻丝弯成一圆环,A、B、C三点将圆环三等分,所以AB段的电阻RADB=
解:阻值为R的电阻丝弯成一圆环,A、B、C三点将圆环三等分,所以AB段的电阻RADB=| 1 |
| 3 |
| 2 |
| 3 |
∵两段导体并联,
∴
| 1 |
| R并 |
| 1 |
| RADB |
| 1 |
| RACB |
即:
| 1 |
| R并 |
| 1 | ||
|
| 1 | ||
|
解得:R并=
| 2 |
| 9 |
| 2 |
| 9 |
则通过圆环的总电:I=
| U |
| R并 |
| 3V |
| 20Ω |
故答案为:0.15.
点评:本题考查了欧姆定律的应用、并联电阻的求法,能够正确判断AB间电路的连接情况是本题的关键.

练习册系列答案
相关题目
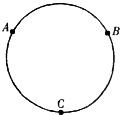 如图所示的圆环是由阻值R、粗细均匀的金属丝制成的.A、B、C三点将圆环分成三等份(每等份电阻为
如图所示的圆环是由阻值R、粗细均匀的金属丝制成的.A、B、C三点将圆环分成三等份(每等份电阻为 如图所示的圆环是由阻值粗细均匀的金属丝制成的.A、B、C三点将圆环分成三等份(每等份电阻为R),若将其中任意两点连入电路,则连入电路的电阻值为
如图所示的圆环是由阻值粗细均匀的金属丝制成的.A、B、C三点将圆环分成三等份(每等份电阻为R),若将其中任意两点连入电路,则连入电路的电阻值为 R),若将其中任意两点连入电路,则连入电路的电阻值为 .
R),若将其中任意两点连入电路,则连入电路的电阻值为 .
 R),若将其中任意两点连入电路,则连入电路的电阻值为 .
R),若将其中任意两点连入电路,则连入电路的电阻值为 .