题目内容
浮在水面上的长方体木块的密度为ρ,水的密度为ρ0,将木块浮在水面以上的部分切去,木块又会上浮,待稳定后再次切去水面以上的部分,剩余木块的体积正好是原来的1/2,则可判断ρ:ρ0为
- A.1:4
- B.1:3
- C.1:2
- D.1:

D
分析:由于木块漂浮,利用阿基米德原理和物体的漂浮条件可得F浮=ρ水v排g=G木=ρ木v木g,得出两种情况下的关系式,再根据切去水上部分后剩余部分的体积等于没切去时排开水的体积、最后剩余木块的体积正好是原来的 ,得出木块和水的密度的大小关系.
,得出木块和水的密度的大小关系.
解答:设原来木块的体积为v,
∵原来木块漂浮在水面上,
∴F浮=G排=G木,
∴ρ水v排1g=ρ木vg,
切去水上部分后,木块的体积为v′,仍漂浮,此时木块的体积:
v′=v排1,
∴ρ水v排1g=ρ水v′g=ρ木vg,
可得ρ木vg=ρ水v′g,----------------①
再切去水上部分,剩余木块的体积等于第二次排开水的体积,
由题知,v剩=v排2= v,
v,
此时:ρ水v排2g=ρ水 vg=ρ木v′g,
vg=ρ木v′g,
可得:ρ水 vg=ρ木v′g,----------------②
vg=ρ木v′g,----------------②
 得:
得:
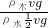 =
= ,
,
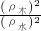 =
=
∴ =
= .
.
故选D.
点评:本题考查了学生对阿基米德原理和物体的漂浮条件的掌握和运用,分析题意得出切去水上部分后,剩余部分的体积等于没切去时排开水的体积是本题的关键.
分析:由于木块漂浮,利用阿基米德原理和物体的漂浮条件可得F浮=ρ水v排g=G木=ρ木v木g,得出两种情况下的关系式,再根据切去水上部分后剩余部分的体积等于没切去时排开水的体积、最后剩余木块的体积正好是原来的
 ,得出木块和水的密度的大小关系.
,得出木块和水的密度的大小关系.解答:设原来木块的体积为v,
∵原来木块漂浮在水面上,
∴F浮=G排=G木,
∴ρ水v排1g=ρ木vg,
切去水上部分后,木块的体积为v′,仍漂浮,此时木块的体积:
v′=v排1,
∴ρ水v排1g=ρ水v′g=ρ木vg,
可得ρ木vg=ρ水v′g,----------------①
再切去水上部分,剩余木块的体积等于第二次排开水的体积,
由题知,v剩=v排2=
 v,
v,此时:ρ水v排2g=ρ水
 vg=ρ木v′g,
vg=ρ木v′g,可得:ρ水
 vg=ρ木v′g,----------------②
vg=ρ木v′g,----------------② 得:
得: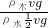 =
= ,
,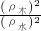 =
=
∴
 =
= .
.故选D.
点评:本题考查了学生对阿基米德原理和物体的漂浮条件的掌握和运用,分析题意得出切去水上部分后,剩余部分的体积等于没切去时排开水的体积是本题的关键.

练习册系列答案
相关题目
 21、具有“世界第一跨”之称的重庆石板坡长江大桥复线桥主跨跨度为330m,复线桥所需钢箱梁在武汉制造.这是一个长达103m、重达1 400t,能浮在水面上却没有动力的大家伙.如图所示为今年5月8日钢箱梁在机动船的推动下缓缓驶入三峡船闸时的情景,请根据此情景提出两个与钢箱梁有关的物理问题,并针对所提出的问题做出简答.
21、具有“世界第一跨”之称的重庆石板坡长江大桥复线桥主跨跨度为330m,复线桥所需钢箱梁在武汉制造.这是一个长达103m、重达1 400t,能浮在水面上却没有动力的大家伙.如图所示为今年5月8日钢箱梁在机动船的推动下缓缓驶入三峡船闸时的情景,请根据此情景提出两个与钢箱梁有关的物理问题,并针对所提出的问题做出简答.
 北京奥运会上,如图是中国选手孟关良、杨文军在皮划艇静水项目男子双人划艇500米决赛中夺冠的镜头.通过测量,双人皮划艇(没有载人)浮在水面上时排开水的体积为0.015米3.求:该皮划艇(没有载人)浮在水面上时受到的浮力是多大?若孟关良、杨文军的两个人的质量为170千克,他们坐在艇上静止时,皮划艇受到的浮力和排开水的体积各是多少?
北京奥运会上,如图是中国选手孟关良、杨文军在皮划艇静水项目男子双人划艇500米决赛中夺冠的镜头.通过测量,双人皮划艇(没有载人)浮在水面上时排开水的体积为0.015米3.求:该皮划艇(没有载人)浮在水面上时受到的浮力是多大?若孟关良、杨文军的两个人的质量为170千克,他们坐在艇上静止时,皮划艇受到的浮力和排开水的体积各是多少?