题目内容
 如图所示,电源电压为6V且保持不变,要使电路中电流表的示数为1A,在AB间需接入电阻.但手边只有阻值为:2Ω,4Ω,8Ω,12Ω,24Ω的电阻各一个,怎样用已有电阻组成所需电阻?写出其中两种:
如图所示,电源电压为6V且保持不变,要使电路中电流表的示数为1A,在AB间需接入电阻.但手边只有阻值为:2Ω,4Ω,8Ω,12Ω,24Ω的电阻各一个,怎样用已有电阻组成所需电阻?写出其中两种:(1)
2Ω与4Ω的电阻串联
2Ω与4Ω的电阻串联
;(2)8Ω与24Ω的电阻并联
8Ω与24Ω的电阻并联
.分析:由欧姆定律可求得满足条件的电阻的阻值;则由手中的电阻利用串并联电路的电阻的性质可得出符合条件的连接方法.
解答:解:由欧姆定律可得:
电阻R=
=
=6Ω;即应需要6Ω的电阻才能符合题意;
因串联电路中总电阻等于各部分电阻的和,故可用2Ω、4Ω的电阻串联后组成6Ω;
因并联电路中总电阻的倒数等于各电阻倒数的和,故可取倒数和为
的电阻并联而成,则应取8Ω与24Ω并联即可.
故答案为:(1)取2Ω与4Ω的电阻串联;(2)取8Ω与24Ω的电阻并联.
电阻R=
| U |
| I |
| 6V |
| 1A |
因串联电路中总电阻等于各部分电阻的和,故可用2Ω、4Ω的电阻串联后组成6Ω;
因并联电路中总电阻的倒数等于各电阻倒数的和,故可取倒数和为
| 1 |
| 6 |
故答案为:(1)取2Ω与4Ω的电阻串联;(2)取8Ω与24Ω的电阻并联.
点评:电阻串并联的规律为重点内容,要求我们应能熟练应用;同时要注意总结规律,如并联电路的总电阻小于任一电阻等;同时注意中考中的物理一般只考查简单的串联或并联电路.

练习册系列答案
相关题目
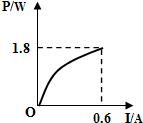
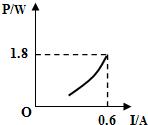
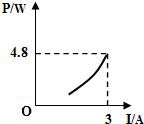
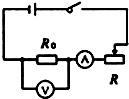 如图所示,电源电压为6V且保持不变,滑动变阻器的最大阻值为20?,定值电阻R0为5?.闭合开关后,移动滑片,发现能使电流表(“0~0.6A”或“0~3A”)和电压表(“0~3V”或“0~15V”)的指针同时达到满刻度线.则R0的电功率与电流的关系图象可能是( )
如图所示,电源电压为6V且保持不变,滑动变阻器的最大阻值为20?,定值电阻R0为5?.闭合开关后,移动滑片,发现能使电流表(“0~0.6A”或“0~3A”)和电压表(“0~3V”或“0~15V”)的指针同时达到满刻度线.则R0的电功率与电流的关系图象可能是( )
 (2013?徐州模拟)如图所示,电源电压为6V,R1阻值为10Ω,R2阻值为20Ω.R1与R2的连接方式为
(2013?徐州模拟)如图所示,电源电压为6V,R1阻值为10Ω,R2阻值为20Ω.R1与R2的连接方式为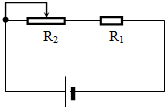 如图所示,电源电压为8V,R1=4Ω,滑动变阻器的最大阻值是12Ω,滑片滑到左端时,通过R1的电流为
如图所示,电源电压为8V,R1=4Ω,滑动变阻器的最大阻值是12Ω,滑片滑到左端时,通过R1的电流为 如图所示,电源电压为6V.开关S闭合时,只有一个灯泡发光,且电压表示数为6V,出现这种情况的原因可能是( )
如图所示,电源电压为6V.开关S闭合时,只有一个灯泡发光,且电压表示数为6V,出现这种情况的原因可能是( )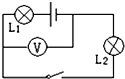 如图所示,电源电压为6V且保持不变.当开关闭合时,电压表的示数为2V,则:
如图所示,电源电压为6V且保持不变.当开关闭合时,电压表的示数为2V,则: