题目内容
 如图所示,甲、乙两个均匀实心正方体放在水平地面上,它们对地面的压强关系为p甲=p乙.若分别沿水平方向截去体积相等的部分后,它们对地面的压强变为p甲′和p乙′,则
如图所示,甲、乙两个均匀实心正方体放在水平地面上,它们对地面的压强关系为p甲=p乙.若分别沿水平方向截去体积相等的部分后,它们对地面的压强变为p甲′和p乙′,则
- A.p甲′=p乙′
- B.p甲′>p乙′
- C.p甲′<p乙′
- D.以上都有可能
C
分析:此题涉及横切问题,由于两个物体都是规则的实心柱状物体,可利用P=ρgh先判断出两个物体的密度大小,然后表示出切除相同高度后,剩余部分对水平面的压强,再做比较.
解答:由P=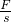 =
= =
= =
= =ρgh;
=ρgh;
∵两物体对水平面的压强相同,即 P=ρ甲gh甲=ρ乙gh乙,且h乙>h甲,
∴ρ乙<ρ甲;
当从水平方向截去相同体积后,甲的底面积小于乙的底面积,所以截取的甲的高度h甲′大于乙截取的高度h乙′:
剩余的甲物体对水平面的压强:p甲′=ρ甲g(h甲-h甲′)=P-ρ甲gh甲′;
剩余的乙物体对水平面的压强p乙′=ρ乙g(h乙-h乙′)=P-ρ乙gh乙′;
因为ρ甲gh甲′>ρ乙gh乙′;
所以p甲′<p乙′.
故选C.
点评:此题是典型的柱状固体的压强问题,要根据已知条件,灵活选用压强计算式P=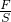 和P=ρgh(适用于实心柱体对支撑面的压强)进行分析解答.
和P=ρgh(适用于实心柱体对支撑面的压强)进行分析解答.
分析:此题涉及横切问题,由于两个物体都是规则的实心柱状物体,可利用P=ρgh先判断出两个物体的密度大小,然后表示出切除相同高度后,剩余部分对水平面的压强,再做比较.
解答:由P=
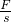 =
= =
= =
= =ρgh;
=ρgh;∵两物体对水平面的压强相同,即 P=ρ甲gh甲=ρ乙gh乙,且h乙>h甲,
∴ρ乙<ρ甲;
当从水平方向截去相同体积后,甲的底面积小于乙的底面积,所以截取的甲的高度h甲′大于乙截取的高度h乙′:
剩余的甲物体对水平面的压强:p甲′=ρ甲g(h甲-h甲′)=P-ρ甲gh甲′;
剩余的乙物体对水平面的压强p乙′=ρ乙g(h乙-h乙′)=P-ρ乙gh乙′;
因为ρ甲gh甲′>ρ乙gh乙′;
所以p甲′<p乙′.
故选C.
点评:此题是典型的柱状固体的压强问题,要根据已知条件,灵活选用压强计算式P=
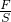 和P=ρgh(适用于实心柱体对支撑面的压强)进行分析解答.
和P=ρgh(适用于实心柱体对支撑面的压强)进行分析解答. 
练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 5、如图所示,甲、乙两个房间里的相同的两壶水放在相同的电炉上都已烧开,我们可以根据所观察的
5、如图所示,甲、乙两个房间里的相同的两壶水放在相同的电炉上都已烧开,我们可以根据所观察的 (2013?亳州模拟)如图所示,甲、乙两个均匀实心正方体分别放置在水平地面上,且它们各自对地面的压强相等.若分别在两个正方体的上部,沿水平方向截去相同高度后,则甲、乙的剩余部分对地面的压强P以及剩余部分质量m的大小关系为( )
(2013?亳州模拟)如图所示,甲、乙两个均匀实心正方体分别放置在水平地面上,且它们各自对地面的压强相等.若分别在两个正方体的上部,沿水平方向截去相同高度后,则甲、乙的剩余部分对地面的压强P以及剩余部分质量m的大小关系为( ) (2013?广安)用四只完全相同的滑轮和两根相同的绳子组成如图所示的甲、乙两个滑轮组,分别将两个相同的钩码提升10cm,若不计绳子与滑轮的摩擦,
(2013?广安)用四只完全相同的滑轮和两根相同的绳子组成如图所示的甲、乙两个滑轮组,分别将两个相同的钩码提升10cm,若不计绳子与滑轮的摩擦, 如图所示,甲、乙两个电磁铁靠近放置,a、b和f、d分别接电源,那么( )
如图所示,甲、乙两个电磁铁靠近放置,a、b和f、d分别接电源,那么( ) 用四只完全相同的滑轮和两根相同的绳子组成如图所示的甲、乙两个滑轮组,不计绳子与滑轮的摩擦,则( )
用四只完全相同的滑轮和两根相同的绳子组成如图所示的甲、乙两个滑轮组,不计绳子与滑轮的摩擦,则( )