题目内容
如图所示,杠杆质量忽略不计,O为杠杆AB的支点,物块甲和乙分别挂在杠杆A、B两端,杠杆平衡,已知物块甲、乙的体积之比是3:2,物块甲的密度ρ甲=2×103kg/m3,乙的密度ρ乙=5×103kg/m3.求:OA与OB的长度之比.
【答案】分析:(1)根据G=mg=ρVg计算出甲、乙两物体的重力;
(2)根据杠杆平衡条件F1L1=F2L2,得出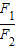 =
=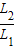 ,代入已知条件,得出OA和OB的长度之比.
,代入已知条件,得出OA和OB的长度之比.
解答:解:G甲=ρ甲V甲g,G乙=ρ乙V乙g,
由杠杆平衡条件得:
G甲OA=G乙OB
则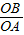 =
=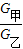 =
=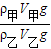 =
=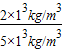 ×
× =
=
所以OA:OB=5:3.
答:OA与OB的长度之比为5:3.
点评:此题是有关杠杆平衡条件的应用,掌握杠杆平衡条件,代入公式时,注意力和力臂的对应,同时涉及到了有关密度、质量的计算.
(2)根据杠杆平衡条件F1L1=F2L2,得出
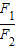 =
=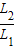 ,代入已知条件,得出OA和OB的长度之比.
,代入已知条件,得出OA和OB的长度之比.解答:解:G甲=ρ甲V甲g,G乙=ρ乙V乙g,
由杠杆平衡条件得:
G甲OA=G乙OB
则
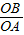 =
=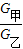 =
=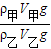 =
=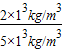 ×
× =
=
所以OA:OB=5:3.
答:OA与OB的长度之比为5:3.
点评:此题是有关杠杆平衡条件的应用,掌握杠杆平衡条件,代入公式时,注意力和力臂的对应,同时涉及到了有关密度、质量的计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




