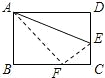
 如图:把边长为AD=10cm,AB=8cm的矩形沿着AE为折痕对折,使点D落在BC上的点F处,则DE的长为( )
如图:把边长为AD=10cm,AB=8cm的矩形沿着AE为折痕对折,使点D落在BC上的点F处,则DE的长为( )| A、3cm | B、4cm | C、5cm | D、6cm |
函数y=
中自变量x的取值范围是( )
| ||
| 5+x |
| A、x≥3 |
| B、x≥3且x≠-5 |
| C、x≥-3且x≠5 |
| D、x≥-3且x≠5 |
点A(2-
,2-
)在( )
| 3 |
| 5 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
| 16 |
| A、2 | B、±2 | C、16 | D、±16 |
如图,OB、OC分别为∠ABC,∠ACB的平分线,∠BOC随着∠A的变化而变化.为探究∠A和∠BOC的关系,现采取如下两种方案,在变化过程中,设∠A为x°,∠BOC为y°.
方案甲:用量角器量出∠A、∠BOC的不断变化时的具体数据,并列表如下: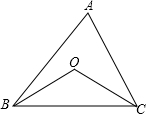
建立直角坐标系,并描点、连线,猜测y与x之间的函数关系,求出y与x的函数关系式.
方案乙:利用角平分线的性质及三角形内角和为180°的性质,直接进行计算,求出y与x之间的函数关系.
(1)若x=60°,则y= .(请直接写 出结果)
出结果)
(2)请采用方案甲或方案乙中的一种进行解答,得到∠A与∠BOC之间的关系.
0 68002 68010 68016 68020 68026 68028 68032 68038 68040 68046 68052 68056 68058 68062 68068 68070 68076 68080 68082 68086 68088 68092 68094 68096 68097 68098 68100 68101 68102 68104 68106 68110 68112 68116 68118 68122 68128 68130 68136 68140 68142 68146 68152 68158 68160 68166 68170 68172 68178 68182 68188 68196 366461
方案甲:用量角器量出∠A、∠BOC的不断变化时的具体数据,并列表如下:

| x | 10 | 20 | 30 | 40 | … |
| y | 95 | 100 | 105 | 110 | … |
方案乙:利用角平分线的性质及三角形内角和为180°的性质,直接进行计算,求出y与x之间的函数关系.
(1)若x=60°,则y=
 出结果)
出结果)(2)请采用方案甲或方案乙中的一种进行解答,得到∠A与∠BOC之间的关系.
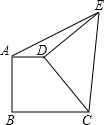 如图直角梯形ABCD中,AD∥BC,AB⊥BC,∠BCD=45°,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )
如图直角梯形ABCD中,AD∥BC,AB⊥BC,∠BCD=45°,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )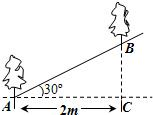 如图,沿倾斜角为30°的山坡植树,要求相邻两棵树的水平距离AC为2m,求相邻两棵树的斜坡距离AB.(精确到0.1m)
如图,沿倾斜角为30°的山坡植树,要求相邻两棵树的水平距离AC为2m,求相邻两棵树的斜坡距离AB.(精确到0.1m) 21、如图,在?ABCD中,E、F分别为BC、AD边上的一点,BE=DF.求证:AE=CF.
21、如图,在?ABCD中,E、F分别为BC、AD边上的一点,BE=DF.求证:AE=CF.