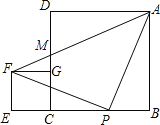
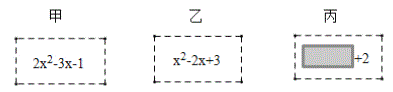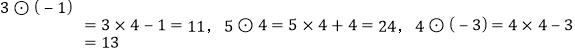【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与![]() ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, ![]() ,2,
,2, ![]() ,2
,2![]() 五种,比n=2时增加了3种,即S=2+3=5.
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+(____) |
5×5 | (________) |
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.

【题目】射击训练班中的甲、乙两名选手在5次射击训练中的成绩依次为(单位:环):
甲:8,8,7,8,9
乙:5,9,7,10,9
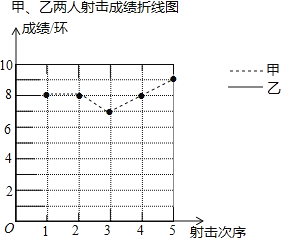
教练根据他们的成绩绘制了如下尚不完整的统计图表:
选手 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 8 | b | 8 | 0.4 |
乙 | α | 9 | c | 3.2 |
根据以上信息,请解答下面的问题:
(1)α= ,b= ,c= ;
(2)完成图中表示乙成绩变化情况的折线;
(3)教练根据这5次成绩,决定选择甲参加射击比赛,教练的理由是什么?
(4)若选手乙再射击第6次,命中的成绩是8环,则选手乙这6次射击成绩的方差与前5次射击成绩的方差相比会 .(填“变大”、“变小”或“不变”)