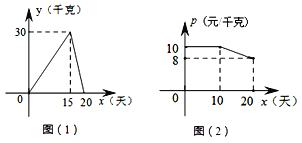
0 339235 339243 339249 339253 339259 339261 339265 339271 339273 339279 339285 339289 339291 339295 339301 339303 339309 339313 339315 339319 339321 339325 339327 339329 339330 339331 339333 339334 339335 339337 339339 339343 339345 339349 339351 339355 339361 339363 339369 339373 339375 339379 339385 339391 339393 339399 339403 339405 339411 339415 339421 339429 366461