甲.乙两位同学五次数学测验成绩如下表：

请你在表中的空白处填上适当的数，用学到的统计知识对两位同学的成绩进行分析，并写出一条合理化建议．

阅读下列材料：

为了在甲、乙两名学生中选拔一人参加数学竞赛，在相同条件下，对他们进行了10次测验，成绩如下：（单位：分）

回答下列问题：

（1）甲学生成绩的众数是_______（分），乙学生成绩的中位数是_______（分）．

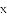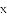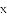（2）若甲学生成绩的平均数是甲，乙学生成绩的平均数是乙，则甲与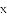乙的大小关系是：________．

（3）经计算知：S2甲=13.2，S2乙=26.36，这表明____________（用简明的文字语言表述）

（4）若测验分数在85分（含85分）以上为优秀，则甲的优秀率为________；乙的优秀率为________．

为选派一名学生参加全市实践活动技能竞赛，A，B两位同学在校实习基地现场进行加工直径为20mm的零件的测试，他俩加工的10个零件的相关数据依次如下图表所示（单位：mm）．

根据测试得到的有关数据，试解答下列问题：

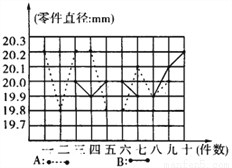
（1）考虑平均数与完全符合要求的个数，你认为________的成绩好些．

（2）计算出S2B的大小，考虑平均数与方差，说明谁的成绩好些．

（3）考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况，你认为派谁去参赛较合适？说明你的理由．

一次期中考试中，甲、乙、丙、丁、戊五位同学的数学、英语成绩等有关信息如下表所示：（单位：分）

（1）求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差；

（2）为了比较不同学科考试成绩的好与差，采用标准分是一个合理的选择，标准分的计算公式：

标准分=（个人成绩一平均成绩）÷成绩标准差．

从标准分看，标准分大的考试成绩更好，请问甲同学在本次考试中，数学与英语哪个学科考得更好？

为了配合“八荣八耻”宣传教育，针对闯红灯的现象时有发生的实际情况，八年级某班开展一次题为“红灯与绿灯”的课题学习活动，它们将全班学生分成8个小组，其中第①～⑥组分别负责早.中.晚三个时段闯红灯违章现象的调查，第⑦小组负责查阅有关红绿灯的交通法规，第⑧小组负责收集有关的交通标志. 数据汇总如下：

回答下列问题：

（1）请你写出2条交通法规：

① .

② .

（2）画出2枚交通标志并说明标志的含义.

标志含义: 标志含义:

（3）早晨.中午.晚上三个时段每分钟车流量的极差是 ，这三个时段的车流总量的中位数是 .

（4）观察表中的数据及条形统计图，写出你发现的一个现象并分析其产生的原因.

（5）通过分析写一条合理化建议.

下列各方程中，是一元二次方程的是（　　）

A. 3x+2=3 B. x3+2x+1=0 C. x2=1 D. x2+2y=0

下列立体图形中，主视图、左视图和俯视图都是矩形的是（　　）

A. B. C. D.

如图，身高1.6米的学生小李想测量学校的旗杆的高度，当他站在C处时，他头顶端的影子正好与旗杆顶端的影子重合，并测得AC=2米，BC=8米，则旗杆的高度是（　　）

A. 6.4米 B. 7米 C. 8米 D. 9米

从长度分别为2，4，6，7的四条线段中随机取三条，能构成三角形的概率是（　　）

A. B. C. D.

若关于x的方程kx2﹣3x﹣ =0有实数根，则实数k的取值范围是（　　）

A. k=0 B. k≥﹣1且k≠0 C. k≥﹣1 D. k＞﹣1