在平面直角坐标系中,点 (-3,4) 关于y轴对称的点的坐标是__________.
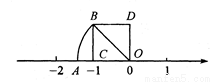
(3,4) 【解析】根据平面直角坐标系中关于y轴成轴对称的点的坐标特点解答. 【解析】 ∵点P(m,n)关于y轴对称点的坐标P′(?m,n), ∴点P(?3,4)关于y轴对称的点的坐标为(3,4). 故答案为:(3,4).如图,在正方形ODBC中,若OC=1,OA=OB,则数轴上点A表示的数是__________.
某人一天饮水1890mL,用四舍五入法对1890mL精确到1000mL表示为____mL.
查看答案在平面直角坐标系中,点(2,-3)在第____象限.
查看答案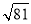 的平方根为_____.
的平方根为_____.
关于直线l:y=kx+k(k≠0),下列说法不正确的是( )
A. 点(0,k)在l上
B. l经过定点(-1,0)
C. 当k>0时,y随x的增大而增大
D. l经过第一、二、三象限
查看答案 试题属性- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知a、b、c是△ABC的三边长,且满足关系式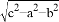 +|a﹣b|=0,则△ABC的形状为_____.
+|a﹣b|=0,则△ABC的形状为_____.
在平面直角坐标系中,点 (-3,4) 关于y轴对称的点的坐标是__________.
查看答案如图,在正方形ODBC中,若OC=1,OA=OB,则数轴上点A表示的数是__________.

某人一天饮水1890mL,用四舍五入法对1890mL精确到1000mL表示为____mL.
查看答案在平面直角坐标系中,点(2,-3)在第____象限.
查看答案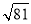 的平方根为_____.
的平方根为_____.
- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
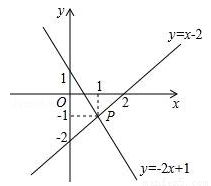
如图,已知函数y=x-2和y=-2x+1的图象交于点P,根据图象可得方程组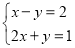 的解是 .
的解是 .
已知a、b、c是△ABC的三边长,且满足关系式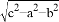 +|a﹣b|=0,则△ABC的形状为_____.
+|a﹣b|=0,则△ABC的形状为_____.
在平面直角坐标系中,点 (-3,4) 关于y轴对称的点的坐标是__________.
查看答案如图,在正方形ODBC中,若OC=1,OA=OB,则数轴上点A表示的数是__________.

某人一天饮水1890mL,用四舍五入法对1890mL精确到1000mL表示为____mL.
查看答案在平面直角坐标系中,点(2,-3)在第____象限.
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
将一次函数y=-x+3的图像沿y轴向下平移2个单位长度,所得图像对应的函数表达式为__________.
y=-x+1 【解析】直接利用一次函数平移规律“上加下减”即可得出答案. 【解析】 ∵将一次函数y=?x+3的图象沿y轴向下平移2个单位长度, ∴平移后所得图象对应的函数关系式为:y=?x+3?2, 即y=?x+1. 故答案为y=?x+1. 点睛:本题考查一次函数图象平移相关知识.利用一次函数平移规律:上加下减,是解题的关键.如图,已知函数y=x-2和y=-2x+1的图象交于点P,根据图象可得方程组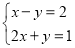 的解是 .
的解是 .

已知a、b、c是△ABC的三边长,且满足关系式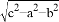 +|a﹣b|=0,则△ABC的形状为_____.
+|a﹣b|=0,则△ABC的形状为_____.
在平面直角坐标系中,点 (-3,4) 关于y轴对称的点的坐标是__________.
查看答案如图,在正方形ODBC中,若OC=1,OA=OB,则数轴上点A表示的数是__________.

某人一天饮水1890mL,用四舍五入法对1890mL精确到1000mL表示为____mL.
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
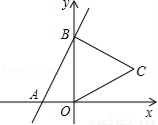
如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 .
将一次函数y=-x+3的图像沿y轴向下平移2个单位长度,所得图像对应的函数表达式为__________.
查看答案如图,已知函数y=x-2和y=-2x+1的图象交于点P,根据图象可得方程组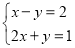 的解是 .
的解是 .

已知a、b、c是△ABC的三边长,且满足关系式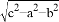 +|a﹣b|=0,则△ABC的形状为_____.
+|a﹣b|=0,则△ABC的形状为_____.
在平面直角坐标系中,点 (-3,4) 关于y轴对称的点的坐标是__________.
查看答案如图,在正方形ODBC中,若OC=1,OA=OB,则数轴上点A表示的数是__________.

- 题型:填空题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
求下列各式中的x.
(1)4x2 =81;
(2)(x+1)3-27=0.
(3)计算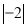 +(3-π)0-2-1+
+(3-π)0-2-1+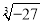
如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 .

将一次函数y=-x+3的图像沿y轴向下平移2个单位长度,所得图像对应的函数表达式为__________.
查看答案如图,已知函数y=x-2和y=-2x+1的图象交于点P,根据图象可得方程组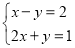 的解是 .
的解是 .

已知a、b、c是△ABC的三边长,且满足关系式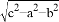 +|a﹣b|=0,则△ABC的形状为_____.
+|a﹣b|=0,则△ABC的形状为_____.
在平面直角坐标系中,点 (-3,4) 关于y轴对称的点的坐标是__________.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
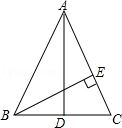
如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
求下列各式中的x.
(1)4x2 =81;
(2)(x+1)3-27=0.
(3)计算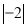 +(3-π)0-2-1+
+(3-π)0-2-1+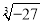
如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 .

将一次函数y=-x+3的图像沿y轴向下平移2个单位长度,所得图像对应的函数表达式为__________.
查看答案如图,已知函数y=x-2和y=-2x+1的图象交于点P,根据图象可得方程组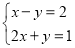 的解是 .
的解是 .

已知a、b、c是△ABC的三边长,且满足关系式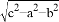 +|a﹣b|=0,则△ABC的形状为_____.
+|a﹣b|=0,则△ABC的形状为_____.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
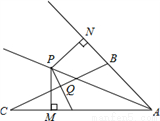
如图,在△ABC中,∠BAC的平分线与BC的垂直平分线PQ相交于点P,过点P分别作PN⊥AB,PM⊥AC,垂足分别为点N,M.求证:BN=CM
如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.

求下列各式中的x.
(1)4x2 =81;
(2)(x+1)3-27=0.
(3)计算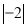 +(3-π)0-2-1+
+(3-π)0-2-1+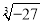
如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 .

将一次函数y=-x+3的图像沿y轴向下平移2个单位长度,所得图像对应的函数表达式为__________.
查看答案如图,已知函数y=x-2和y=-2x+1的图象交于点P,根据图象可得方程组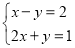 的解是 .
的解是 .

- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
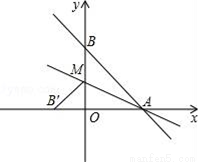
如图,直线y=﹣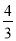 x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.求:
x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.求:
(1)点B′的坐标;
(2)直线AM所对应的函数关系式.
如图,在△ABC中,∠BAC的平分线与BC的垂直平分线PQ相交于点P,过点P分别作PN⊥AB,PM⊥AC,垂足分别为点N,M.求证:BN=CM

如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.

求下列各式中的x.
(1)4x2 =81;
(2)(x+1)3-27=0.
(3)计算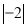 +(3-π)0-2-1+
+(3-π)0-2-1+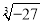
如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 .

将一次函数y=-x+3的图像沿y轴向下平移2个单位长度,所得图像对应的函数表达式为__________.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
甲乙两人在同一条道路上同时出发,同时行进,甲步行,乙骑车,出发时甲在前,乙在后,图中l甲,l乙,分别表示出发后甲、乙离出发地的路程s(km)和经历的时间t(h)的关系.
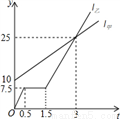
(1)乙出发时甲、乙相距___km.
(2)乙骑行一段路后,自行车发生故障,进行修理,所用的时间是___h.
(3)图象l甲,l乙相交的实际意义是什么?
(4)若乙的自行车没有故障,保持出发时的速度前进,求甲,乙相遇的时间和地点.
(1)10;(2)1;(3) 乙出发3小时时,在距乙出发点25km处,乙追上甲;(4) 在距乙的出发点15km处,乙追上甲. 【解析】(1)根据图象,当t=0时,两个函数的图象的纵坐标的差就是所求; (2)根据乙的图象即可直接求解; (3)根据横纵坐标的实际应用是关键; (4)利用待定系数法求得甲的函数解析式以及乙出发时y与t的函数解析式,然后解两个解析式组成的方程组即可求...如图,直线y=﹣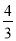 x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.求:
x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.求:
(1)点B′的坐标;
(2)直线AM所对应的函数关系式.

如图,在△ABC中,∠BAC的平分线与BC的垂直平分线PQ相交于点P,过点P分别作PN⊥AB,PM⊥AC,垂足分别为点N,M.求证:BN=CM

如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.

求下列各式中的x.
(1)4x2 =81;
(2)(x+1)3-27=0.
(3)计算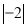 +(3-π)0-2-1+
+(3-π)0-2-1+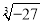
如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 .

- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧