青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间比淡季上涨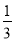 ,下表是去年该酒店豪华间某两天的相关记录:
,下表是去年该酒店豪华间某两天的相关记录:
旺季 | 淡季 | |
未入住房间数 | 10 | 0 |
日总收入(元) | 24 000 | 40 000 |
(1)该酒店豪华间有多少间?旺季每间价格为多少元
(2)今年旺季来临,豪华间的间数不变。经市场调查发现,如果豪华间仍旧实行去年旺季价格,那么每天都客满;如果价格继续上涨,那么每增加25元,每天未入住房间数增加1间。不考虑其他因素,该酒店将豪华间的价格上涨多少元时,豪华间的日总收入最高?最高日总收入是多少元?
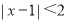 的解集
的解集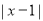 的几何意义
的几何意义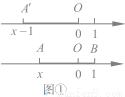
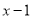 ,由绝对值的定义可知,点A'与O的距离为
,由绝对值的定义可知,点A'与O的距离为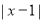 ,
,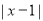 。将线段A'O向右平移一个单位,得到线段AB,,此时点A对应的数为
。将线段A'O向右平移一个单位,得到线段AB,,此时点A对应的数为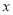 ,点B的对应数是1,
,点B的对应数是1,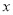 所对应的点A与1所对应的点B之间的距离AB。
所对应的点A与1所对应的点B之间的距离AB。 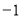 所对应的点与1所对应的点之间的距离都为2,所以方程的解为
所对应的点与1所对应的点之间的距离都为2,所以方程的解为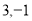
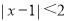 的解集
的解集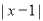 表示数轴上
表示数轴上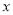 所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点所对应的数
所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点所对应的数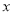 的范围。
的范围。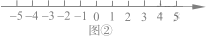
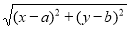 的几何意义
的几何意义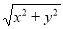 的几何意义
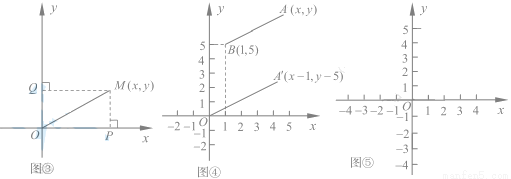
的几何意义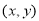 ,过M作MP⊥x轴于P,作MQ⊥y轴于Q,则点P点坐标(
,过M作MP⊥x轴于P,作MQ⊥y轴于Q,则点P点坐标(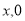 ),Q点坐标(
),Q点坐标(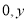 ),|OP|=
),|OP|=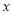 ,|OQ|=
,|OQ|=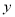 ,
,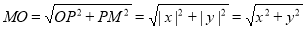
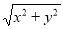 的几何意义可以理解为点M
的几何意义可以理解为点M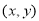 与原点O(0,0)之间的距离OM
与原点O(0,0)之间的距离OM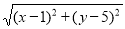 的几何意义
的几何意义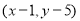 ,由探究(二)(1)可知,
,由探究(二)(1)可知,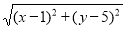 ,将线段 A'O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时A的坐标为(
,将线段 A'O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时A的坐标为(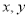 ),点B的坐标为(1,5)。
),点B的坐标为(1,5)。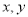 )与点B(1,5)之间的距离。
)与点B(1,5)之间的距离。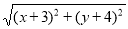 的几何意义
的几何意义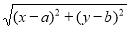 的几何意义可以理解为:_________________________.
的几何意义可以理解为:_________________________.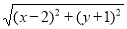 +
+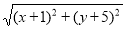 的几何意义可以理解为:点A
的几何意义可以理解为:点A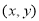 与点E
与点E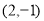 的距离与点AA
的距离与点AA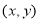 与点F____________(填写坐标)的距离之和。
与点F____________(填写坐标)的距离之和。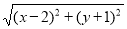 +
+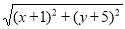 的最小值为____________(直接写出结果)
的最小值为____________(直接写出结果)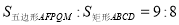 ?若存在,求出 t 的值;若不存在,请说明理由;
?若存在,求出 t 的值;若不存在,请说明理由;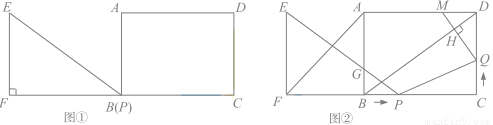
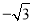 ,
,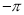 ,-1,其中最小的数是( )
,-1,其中最小的数是( )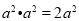 B.
B.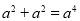
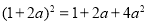 D.
D.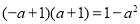

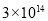 美元 B.
美元 B.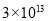 美元 C.
美元 C. 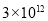 美元 D.
美元 D.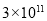 美元
美元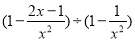 的结果为( )
的结果为( )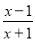 B.
B.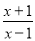 C.
C.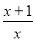 D.
D.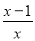
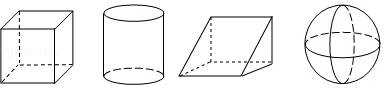
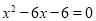 配方后化为( )
配方后化为( )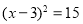 B.
B.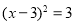 C.
C. 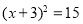 D.
D.