二次函数y=ax2+b（b＞0）与反比例函数y=
在同一坐标系中的图象可能是（ ）
|
| A． |
| B． |
| C． |
| D． |
|
如图，M，N两点在数轴上表示的数分别是m，n，则下列式子中成立的是（ ）
|
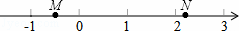
| A． | m+n＜0 | B． | ﹣m＜﹣n | C． | |m|﹣|n|＞0 | D． | 2+m＜2+n |
如图，在4×4的正方形网格中，每个小正方形的边长为1，若将△AOC绕点O顺时针旋转90°得到△BOD，则
的长为（ ）
|
| A． | π | B． | 6π | C． | 3π | D． | 1.5π |
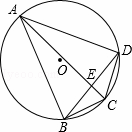
如图，点A，B，C，D都在⊙O上，AC，BD相交于点E，则∠ABD=（ ）
|
| A． | ∠ACD | B． | ∠ADB | C． | ∠AED | D． | ∠ACB |
要使分式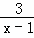
有意义，则的取值范围是（ ）
|
| A． | x≠1 | B． | x＞1 | C． | x＜1 | D． | x≠﹣1 |
如图，在△ABC中，AB=AC，∠A=30°，以B为圆心，BC的长为半径圆弧，交AC于点D，连接BD，则∠ABD=（ ）
|
| A． | 30 | B． | 45 | C． | 60 | D． | 90 |
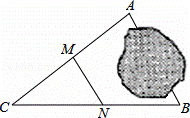
如图，A，B两地被池塘隔开，小明通过下列方法测出了A、B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测量出MN的长为12m，由此他就知道了A、B间的距离．有关他这次探究活动的描述错误的是（ ）
|
| A． | AB=24m | B． | MN∥AB | C． | △CMN∽△CAB | D． | CM：MA=1：2 |
下列计算正确的是（ ）
|
| A． | a+2a2=3a3 | B． | a3•a2=a6 | C． | a6+a2=a3 | D． | （ab）3=a3b3 |
已知三角形两边长分别为3和8，则该三角形第三边的长可能是（ ）
|
| A． | 5 | B． | 10 | C． | 11 | D． | 12 |