0 20034 20042 20048 20052 20058 20060 20064 20070 20072 20078 20084 20088 20090 20094 20100 20102 20108 20112 20114 20118 20120 20124 20126 20128 20129 20130 20132 20133 20134 20136 20138 20142 20144 20148 20150 20154 20160 20162 20168 20172 20174 20178 20184 20190 20192 20198 20202 20204 20210 20214 20220 20228 366461
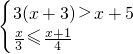 ,并写出不等式组的所有整数解.
,并写出不等式组的所有整数解. 完成下列推理过程:
完成下列推理过程:
 上任意一点.求证:PB+PC=PA;
上任意一点.求证:PB+PC=PA;

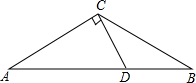 如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D. ,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似?若存在,求出DP的长;若不存在,请说明理由.
,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似?若存在,求出DP的长;若不存在,请说明理由.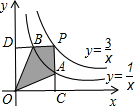 两个反比例函数
两个反比例函数 和y=
和y= 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在 的图象于点A,PD⊥y轴于点D,交
的图象于点A,PD⊥y轴于点D,交