(1)在学习《二次函数的图象和性质》时,我们从“数”和“形”两个方面对二次函数y=x2和y=(x+3)2进行了研究,现在让我们重温这一过程.
①填表(表中阴影部分不需填空):
②从对应点的位置看,函数y=x2的图象与函数y=(x+3)2的图象的位置有什么关系?
(2)借鉴(1)中研究的经验,解决问题:
①把函数y=2x的图象向______(填“左”或“右”)平移______个单位长度可以得到函数y=2x+6的图象.
②直接写出函数y=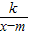 (k、m是常数,k≠0,m>0)的两条不同类型的性质.
(k、m是常数,k≠0,m>0)的两条不同类型的性质.
0 155394 155402 155408 155412 155418 155420 155424 155430 155432 155438 155444 155448 155450 155454 155460 155462 155468 155472 155474 155478 155480 155484 155486 155488 155489 155490 155492 155493 155494 155496 155498 155502 155504 155508 155510 155514 155520 155522 155528 155532 155534 155538 155544 155550 155552 155558 155562 155564 155570 155574 155580 155588 366461
①填表(表中阴影部分不需填空):
| x | … | -6 | -5 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | … | |
| y=x2 | … | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | … | |||
| y=(x+3)2 | … | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | … |
(2)借鉴(1)中研究的经验,解决问题:
①把函数y=2x的图象向______(填“左”或“右”)平移______个单位长度可以得到函数y=2x+6的图象.
②直接写出函数y=
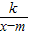 (k、m是常数,k≠0,m>0)的两条不同类型的性质.
(k、m是常数,k≠0,m>0)的两条不同类型的性质.



 ≈1.73,sin27°≈0.45,cos27°≈0.89,tan27°≈0.50)
≈1.73,sin27°≈0.45,cos27°≈0.89,tan27°≈0.50)


 ,请你帮助该小组求出a可能的最大整数值.
,请你帮助该小组求出a可能的最大整数值.
 的大小关系.
的大小关系. =( )
=( )