如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm．P为BC的中点，动点Q从点P出发，沿射线PC方向以2cm/s的速度运动，以P为圆心，PQ长为半径作圆．设点Q运动的时间为t s．
某市“希望”中学为了了解学生“大间操”的活动情况，在七、八、九年级的学生中，分别抽取相同数量的学生对“你最喜欢的运动项目”进行调查（每人只能选一项）．调查结果的部分数据如下表（图）所示，其中七年级最喜欢跳绳的人数比八年级多5人，九年级最喜欢排球的人数为10人．
七年级学生最喜欢的运动项目人数统计表：
八年级学生最喜欢的运动项目人数统计图：
请根据统计表（图）解答下列问题：
（1）本次调查抽取了多少名学生？
（2）补全统计表和统计图，并求出“最喜欢跳绳”的学生占抽样总人数的百分比；
（3）该校共有学生1800人，学校想对“最喜欢踢毽”的学生每4人提供一个毽，那么学校在“大间操”时至少应提供多少个毽？
七年级学生最喜欢的运动项目人数统计表：
| 项目 | 排球 | 篮球 | 跳绳 | 踢毽 | 其它 |
| 人数（人） | 7 | 8 | 14 | 6 |
请根据统计表（图）解答下列问题：
（1）本次调查抽取了多少名学生？
（2）补全统计表和统计图，并求出“最喜欢跳绳”的学生占抽样总人数的百分比；
（3）该校共有学生1800人，学校想对“最喜欢踢毽”的学生每4人提供一个毽，那么学校在“大间操”时至少应提供多少个毽？
某商场出售一批进价为2元的贺卡，在市场营销中发现，此商品的日销售单价x（单位：元）与日销售数量y（单位：张）之间有如下关系：
（1）根据表中数据在平面直角坐标系中描出实数对（x，y）的对应点；
（2）确定y与x之间的函数关系式，并画出图象；
（3）设销售此贺卡的日纯利润为w元，试求出w与x之间的函数关系式．若物价局规定该贺卡售价最高不超过10元/张，请你求出日销售单价x定为多少元时，才能获得最大日销售利润？
| 销售单价x（元） | 3 | 4 | 5 | 6 |
| 日销售量y（元） | 20 | 15 | 12 | 10 |
（2）确定y与x之间的函数关系式，并画出图象；
（3）设销售此贺卡的日纯利润为w元，试求出w与x之间的函数关系式．若物价局规定该贺卡售价最高不超过10元/张，请你求出日销售单价x定为多少元时，才能获得最大日销售利润？
【问题情境】
已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？
【数学模型】
设该矩形的长为x，周长为y，则y与x的函数关系式为y=2（x+
）（x＞0）．
【探索研究】
（1）我们可以借鉴以前研究函数的经验，先探索函数y=x+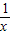
（x＞0）的图象和性质．
①填写下表，画出函数的图象；
②观察图象，写出该函数两条不同类型的性质；
③在求二次函数y=ax2+bx+c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数y=x+
（x＞0）的最小值．
【解决问题】
（2）用上述方法解决“问题情境”中的问题，直接写出答案．
0 153125 153133 153139 153143 153149 153151 153155 153161 153163 153169 153175 153179 153181 153185 153191 153193 153199 153203 153205 153209 153211 153215 153217 153219 153220 153221 153223 153224 153225 153227 153229 153233 153235 153239 153241 153245 153251 153253 153259 153263 153265 153269 153275 153281 153283 153289 153293 153295 153301 153305 153311 153319 366461
已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？
【数学模型】
设该矩形的长为x，周长为y，则y与x的函数关系式为y=2（x+
）（x＞0）．【探索研究】
（1）我们可以借鉴以前研究函数的经验，先探索函数y=x+
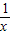（x＞0）的图象和性质．①填写下表，画出函数的图象；
| x | … |  |  |  | 1 | 2 | 3 | 4 | … |
| y | … | … |
③在求二次函数y=ax2+bx+c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数y=x+
（x＞0）的最小值．【解决问题】
（2）用上述方法解决“问题情境”中的问题，直接写出答案．
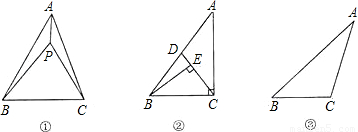
）的结果是（ ）
