某公司在固定线路上运输,拟用运营指数Q量化考核司机的工作业绩.Q=W+100,而W的大小与运输次数n及平均速度x(km/h)有关(不考虑其他因素),W由两部分的和组成:一部分与x的平方成正比,另一部分与x的n倍成正比.试行中得到了表中的数据.
(1)用含x和n的式子表示Q;
(2)当x=70,Q=450时,求n的值;
(3)若n=3,要使Q最大,确定x的值;
(4)设n=2,x=40,能否在n增加m%(m>0)同时x减少m%的情况下,而Q的值仍为420?若能,求出m的值;若不能,请说明理由.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(-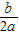 ,
,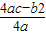 )
)
0 151807 151815 151821 151825 151831 151833 151837 151843 151845 151851 151857 151861 151863 151867 151873 151875 151881 151885 151887 151891 151893 151897 151899 151901 151902 151903 151905 151906 151907 151909 151911 151915 151917 151921 151923 151927 151933 151935 151941 151945 151947 151951 151957 151963 151965 151971 151975 151977 151983 151987 151993 152001 366461
| 次数n | 2 | 1 |
| 速度x | 40 | 60 |
| 指数Q | 420 | 100 |
(2)当x=70,Q=450时,求n的值;
(3)若n=3,要使Q最大,确定x的值;
(4)设n=2,x=40,能否在n增加m%(m>0)同时x减少m%的情况下,而Q的值仍为420?若能,求出m的值;若不能,请说明理由.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(-
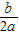 ,
,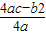 )
)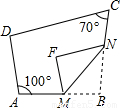 如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B= °.
如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B= °.




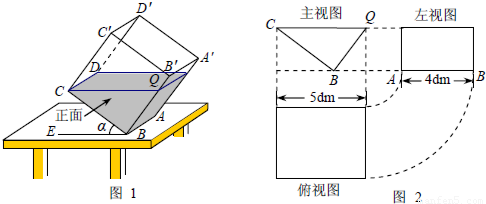
 分别交OA,OB于点M,N.
分别交OA,OB于点M,N. 上,当△AOQ的面积最大时,直接写出∠BOQ的度数.
上,当△AOQ的面积最大时,直接写出∠BOQ的度数.
 ,tan37°=
,tan37°= )
)

 )
) |
| )2
)2 |
|