某校的围墙上端由一段段相同的凹曲拱形栅栏组成，如图所示，其拱形图形为抛物线的一部分，栅栏的跨径AB间，按相同的间距0.2米用5根立柱加固，拱高OC为0.6米．
有一种计算机控制的线切割机床，它可以自动切割只有直线和抛物线组成的零件，工作时只要先确定零件上各点的坐标及线段与抛物线的关系式作为程序输入计算机即可．今有如图所示的零件需按A?B?C?D?A的路径切割，请按下表将程序编完整．
| 线段或抛物线 | 起始坐标 | 关系式 | 终点坐标 |
| 抛物线APB | |||
| 线段BC | （1，0） | x=1 | （1，-1） |
| 线段CD | （1，-1） | ||
| 线段AD | （1，0） |
小明代表班级参加校运会的铅球项目，他想：“怎样才能将铅球推得更远呢”，于是找来小刚做了如下的探索：小明手挚铅球在控制每次推出时用力相同的条件下，分别沿与水平线成30°、45°、60°方向推了三次．铅球推出后沿抛物线形运动．如图，小明推铅球时的出手点距地面2m，以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系，分别得到的有关数据如下表：
（1）请你求出表格中两横线上的数据，写出计算过程，并将结果填入表格中的横线上；
（2）请根据以上数据，对如何将铅球推得更远提出你的建议．
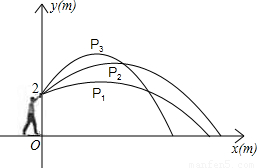
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06（x-3）2+2.5 | y2= ______（x-4）2+3.6 | y3=-0.22（x-3）2+4 |
| 估测铅球在最高点的坐标 | P1（3，2.5） | P2（4，3.6） | P3（3，4） |
| 铅球落点到小明站立处的水平距离 | 9.5m | ______m | 7.3m |
（2）请根据以上数据，对如何将铅球推得更远提出你的建议．
据统计每年由于汽车超速行驶而造成的交通事故是造成人员死亡的主要原因之一．行驶中的汽车，在刹车后由于惯性的原因，还要继续向前滑行一段距离才能停住，这段距离称为“刹车距离”．为了测定某种型号汽车的刹车性能（车速不超过140千米/时），对这种汽车的刹车距离进行测试，测得的数据如下表：
（1）在如图所示的直角坐标系中以车速为x轴，以刹车距离为y轴描出这些数据所表示的点，并用光滑的曲线连接这些点，得到某函数的大致图象．
（2）观察图象估计函数的类型，并确定一个满足这些数据的函数解析式．
（3）一辆该型号的汽车在国道上发生了交通事故，现场测得刹车距离为46.5米，请推测刹车时速度是多少？请问在事故发生时，汽车是否超速行驶？
0 146692 146700 146706 146710 146716 146718 146722 146728 146730 146736 146742 146746 146748 146752 146758 146760 146766 146770 146772 146776 146778 146782 146784 146786 146787 146788 146790 146791 146792 146794 146796 146800 146802 146806 146808 146812 146818 146820 146826 146830 146832 146836 146842 146848 146850 146856 146860 146862 146868 146872 146878 146886 366461
| 刹车时车速（千米/时） | 5 | 10 | 15 | 20 | 25 | 30 | |
| 刹车距离（米） | 0.1 | 0.3 | 0.6 | 1 | 1.5 | 2.1 |
（2）观察图象估计函数的类型，并确定一个满足这些数据的函数解析式．
（3）一辆该型号的汽车在国道上发生了交通事故，现场测得刹车距离为46.5米，请推测刹车时速度是多少？请问在事故发生时，汽车是否超速行驶？
）2+
的形式，并据此说明：当x为何值时，租赁公司出租该型号设备的月收益最大？最大月收益是多少？