水产公司有一种海产品共2 104千克,为寻求合适的销售价格,进行了8天试销,试销情况如下:
观察表中数据,发现可以用反比例函数刻画这种海产品的每天销售量y(千克)与销售价格x(元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量y(千克)与销售价格x(元/千克)之间都满足这一关系.
(1)写出这个反比例函数的解析式,并补全表格;
(2)在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?
(3)在按(2)中定价继续销售15天后,公司发现剩余的这些海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?
0 145864 145872 145878 145882 145888 145890 145894 145900 145902 145908 145914 145918 145920 145924 145930 145932 145938 145942 145944 145948 145950 145954 145956 145958 145959 145960 145962 145963 145964 145966 145968 145972 145974 145978 145980 145984 145990 145992 145998 146002 146004 146008 146014 146020 146022 146028 146032 146034 146040 146044 146050 146058 366461
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | 第8天 | |
| 售价 x(元/千克) | 400 | 250 | 240 | 200 | 150 | 125 | 120 | |
| 销售量 y(千克) | 30 | 40 | 48 | 60 | 80 | 96 | 100 |
(1)写出这个反比例函数的解析式,并补全表格;
(2)在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?
(3)在按(2)中定价继续销售15天后,公司发现剩余的这些海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?
 与双曲线
与双曲线 (k>0)交于A、B两点,且点A的横坐标为4.
(k>0)交于A、B两点,且点A的横坐标为4. (k>0)上一点C的纵坐标为8,求△AOC的面积.
(k>0)上一点C的纵坐标为8,求△AOC的面积.

 的图象交于A、B两点.
的图象交于A、B两点.
 (k≠0)和一次函数y=-x-6.
(k≠0)和一次函数y=-x-6.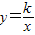 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3.
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3. )
)


