春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第x天(1≤x≤20且x为整数)的捕捞与销售的相关信息如表:
(1)在此期间该养殖场每天的捕捞量与前一天末的捕捞量相比是如何变化的?
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(天)之间的函数关系式?(当天收入=日销售额-日捕捞成本)
(3)试说明(2)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) | 5- |
| 捕捞量(kg) | 950-10x |
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(天)之间的函数关系式?(当天收入=日销售额-日捕捞成本)
(3)试说明(2)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
面对国际金融危机.某铁路旅行社为吸引市民组团去某风景区旅游,现推出如下标准:某单位组织员工去该风景区旅游,设有x人参加,应付旅游费y元.
(1)请写出y与x的函数关系式;
(2)若该单位现有45人,本次旅游至少去26人,则该单位最多应付旅游费多少元?
(1)请写出y与x的函数关系式;
(2)若该单位现有45人,本次旅游至少去26人,则该单位最多应付旅游费多少元?
| 人数 | 不超过25人 | 超过25人但不超过50人 | 超过50人 |
| 人均旅游费 | 1500元 | 每增加1人,人均旅游费降低20元 | 1000元 |
种植能手小李的实验田可种植A种作物或B种作物(A、B两种作物不能同时种植),原来的种植情况如表.通过参加农业科技培训,小李提高了种植技术.现准备在原有的基础上增种,以提高总产量.但根据科学种植的经验,每增种1棵A种或B种作物,都会导致单棵作物平均产量减少0.2千克,而且每种作物的增种数量都不能超过原有数量的80%.设A种作物增种m棵,总产量为yA千克;B种作物增种n棵,总产量为yB千克.
(1)A种作物增种m棵后,单棵平均产量为______千克;B种作物增种n棵后,单棵平均产量为______千克;
(2)求yA与m之间的函数关系式及yB与n之间的函数关系式;
(3)求提高种植技术后,小李增种何种作物可获得最大总产量?最大总产量是多少千克?
0 128065 128073 128079 128083 128089 128091 128095 128101 128103 128109 128115 128119 128121 128125 128131 128133 128139 128143 128145 128149 128151 128155 128157 128159 128160 128161 128163 128164 128165 128167 128169 128173 128175 128179 128181 128185 128191 128193 128199 128203 128205 128209 128215 128221 128223 128229 128233 128235 128241 128245 128251 128259 366461
| 种植品种 数量 | A种作物 | B中作物 |
| 原种植量(棵) | 50 | 60 |
| 原产量(千克/棵) | 30 | 26 |
(2)求yA与m之间的函数关系式及yB与n之间的函数关系式;
(3)求提高种植技术后,小李增种何种作物可获得最大总产量?最大总产量是多少千克?
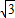 时x的值;
时x的值;
 x+36,而其每千克成本y2(元)与销售月份x(月)满足的函数关系如图所示.
x+36,而其每千克成本y2(元)与销售月份x(月)满足的函数关系如图所示.