在梯形ABCD中.AD∥BC.AB=DC=AD=6.∠ABC=60°.点E.F分别在线段AD.DC上.且∠BEF=120°.设AE=x.DF=y．(1)求y与x的函数表达式,(2)当x——青夏教育精英家教网——

在梯形ABCD中，AD∥BC，AB=DC=AD=6，∠ABC=60°，点E，F分别在线段AD，DC上（点E与点A，D不重合），且∠BEF=120°，设AE=x，DF=y．
（1）求y与x的函数表达式；
（2）当x为何值时，y有最大值，最大值是多少？

如图，点M（4，0），以点M为圆心、2为半径的圆与x轴交于点A、B．已知抛物线y=

x²+bx+c过点A和B，与y轴交于点C．
（1）求点C的坐标，并画出抛物线的大致图象；
（2）点Q（8，m）在抛物线y=

x²+bx+c上，点P为此抛物线对称轴上一个动点，求PQ+PB的最小值；
（3）CE是过点C的⊙M的切线，点E是切点，求OE所在直线的解析式．

实验与探究：
（1）在图1，2，3中，已知平行四边形ABCD的三个顶点A，B，D的坐标（如图所示），求出图1，2，3中的第四个顶点C的坐标，已求出图1中顶点C的坐标是（5，2），图2，3中顶点C的坐标分别是______，______；

（2）在图4中，平行四边形ABCD的顶点A，B，D的坐标（如图所示），求出顶点C的坐标（C点坐标用含a，b，c，d，e，f的代数式表示）；

归纳与发现：
（3）通过对图1，2，3，4的观察和顶点C的坐标的探究，你会发现：无论平行四边形ABCD处于直角坐标系中哪个位置，当其顶点坐标为A（a，b），B（c，d），C（m，n），D（e，f）（如图4）时，则四个顶点的横坐标a，c，m，e之间的等量关系为______；纵坐标b，d，n，f之间的等量关系为______
（不必证明）；运用与推广：
（4）在同一直角坐标系中有抛物线y=x²-（5c-3）x-c和三个点

，H（2c，0）（其中c＞0）．问当c为何值时，该抛物线上存在点P，使得以G，S，H，P为顶点的四边形是平行四边形？并求出所有符合条件的P点坐标．

如图，已知平行四边形ABCD的顶点A的坐标是（0，16），AB平行于x轴，B，C，D三点在抛物线y=

x²上，DC交y轴于N点，一条直线OE与AB交于E点，与DC交于F点，如果E点的横坐标为a，四边形ADFE的面积为

．
（1）求出B，D两点的坐标；
（2）求a的值；
（3）作△ADN的内切圆⊙P，切点分别为M，K，H，求tan∠PFM的值．

已知反比例函数

的图象经过点P（2，2），函数y=ax+b的图象与直线y=-x平行，并且经过反比例函数图象上一点Q（1，m）．
（1）求出点Q的坐标；
（2）函数y=ax²+bx+

有最大值还是最小值？这个值是多少？

如图，已知抛物线y=ax²+bx-3与x轴交于A、B两点，与y轴交于C点，经过A、B、C三点的圆的圆心M（1，m）恰好在此抛物线的对称轴上，⊙M的半径为

．设⊙M与y轴交于D，抛物线的顶点为E．
（1）求m的值及抛物线的解析式；
（2）设∠DBC=α，∠CBE=β，求sin（α-β）的值；
（3）探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形与△BCE相似？若存在，请指出点P的位置，并直接写出点P的坐标；若不存在，请说明理由．

如图，矩形A′BC′O′是矩形OABC（边OA在x轴正半轴上，边OC在y轴正半轴上）绕B点逆时针旋转得到的，O′点在x轴的正半轴上，B点的坐标为（1，3）．
（1）如果二次函数y=ax²+bx+c（a≠0）的图象经过O，O′两点且图象顶点M的纵坐标为-1，求这个二次函数的解析式；
（2）在（1）中求出的二次函数图象对称轴的右支上是否存在点P，使得△POM为直角三角形？若存在，请求出P点的坐标和△POM的面积；若不存在，请说明理由；
（3）求边C′O′所在直线的解析式．

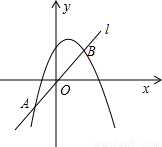
如图，已知直线l：y=

及抛物线C：y=ax²+bx+c（a≠0），且抛物线C图象上部分点的对应值如下表：

x	…	-2	-1	0	1	2	3	4	…
y	…	-5	0	3	4	3	0	-5	…

（1）求抛物线C对应的函数解析式；
（2）求直线l与抛物线C的交点A、B的坐标；
（3）若动点M在直线l上方的抛物线C上移动，求△ABM的边AB上的高h的最大值．

经过x轴上A（-1，0）、B（3，0）两点的抛物线y=ax²+bx+c交y轴于点C，设抛物线的顶点为D，若以DB为直径的⊙G经过点C，求解下列问题：
（1）用含a的代数式表示出C，D的坐标；
（2）求抛物线的解析式；
（3）如图，当a＜0时，能否在抛物线上找到一点Q，使△BDQ为直角三角形？你能写出Q点的坐标吗？

如图，抛物线y=

x²+mx+n交x轴于A、B两点，交y轴于点C，点P是它的顶点，点A的横坐标是-3，点B的横坐标是1．
（1）求m、n的值；
（2）求直线PC的解析式；
（3）请探究以点A为圆心、直径为5的圆与直线PC的位置关系，并说明理由．（参考数：

0 128017 128025 128031 128035 128041 128043 128047 128053 128055 128061 128067 128071 128073 128077 128083 128085 128091 128095 128097 128101 128103 128107 128109 128111 128112 128113 128115 128116 128117 128119 128121 128125 128127 128131 128133 128137 128143 128145 128151 128155 128157 128161 128167 128173 128175 128181 128185 128187 128193 128197 128203 128211 366461