如图,已知直线l:y= 及抛物线C:y=ax2+bx+c(a≠0),且抛物线C图象上部分点的对应值如下表:
及抛物线C:y=ax2+bx+c(a≠0),且抛物线C图象上部分点的对应值如下表:
(1)求抛物线C对应的函数解析式;
(2)求直线l与抛物线C的交点A、B的坐标;
(3)若动点M在直线l上方的抛物线C上移动,求△ABM的边AB上的高h的最大值.

0 126469 126477 126483 126487 126493 126495 126499 126505 126507 126513 126519 126523 126525 126529 126535 126537 126543 126547 126549 126553 126555 126559 126561 126563 126564 126565 126567 126568 126569 126571 126573 126577 126579 126583 126585 126589 126595 126597 126603 126607 126609 126613 126619 126625 126627 126633 126637 126639 126645 126649 126655 126663 366461
 及抛物线C:y=ax2+bx+c(a≠0),且抛物线C图象上部分点的对应值如下表:
及抛物线C:y=ax2+bx+c(a≠0),且抛物线C图象上部分点的对应值如下表:| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | -5 | 0 | 3 | 4 | 3 | 0 | -5 | … |
(2)求直线l与抛物线C的交点A、B的坐标;
(3)若动点M在直线l上方的抛物线C上移动,求△ABM的边AB上的高h的最大值.


 x2+bx+c过点A和B,与y轴交于点C.
x2+bx+c过点A和B,与y轴交于点C. x2+bx+c上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值;
x2+bx+c上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值;


 ,
, ,H(2c,0)(其中c>0).问当c为何值时,该抛物线上存在点P,使得以G,S,H,P为顶点的四边形是平行四边形?并求出所有符合条件的P点坐标.
,H(2c,0)(其中c>0).问当c为何值时,该抛物线上存在点P,使得以G,S,H,P为顶点的四边形是平行四边形?并求出所有符合条件的P点坐标. x2上,DC交y轴于N点,一条直线OE与AB交于E点,与DC交于F点,如果E点的横坐标为a,四边形ADFE的面积为
x2上,DC交y轴于N点,一条直线OE与AB交于E点,与DC交于F点,如果E点的横坐标为a,四边形ADFE的面积为 .
.
 的图象经过点P(2,2),函数y=ax+b的图象与直线y=-x平行,并且经过反比例函数图象上一点Q(1,m).
的图象经过点P(2,2),函数y=ax+b的图象与直线y=-x平行,并且经过反比例函数图象上一点Q(1,m). 有最大值还是最小值?这个值是多少?
有最大值还是最小值?这个值是多少? .设⊙M与y轴交于D,抛物线的顶点为E.
.设⊙M与y轴交于D,抛物线的顶点为E.

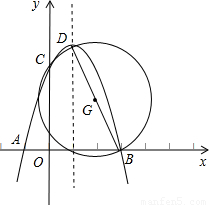
 x2+mx+n交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是-3,点B的横坐标是1.
x2+mx+n交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是-3,点B的横坐标是1. ≈1.41,
≈1.41, ≈1.73,
≈1.73, ≈2.24)
≈2.24)