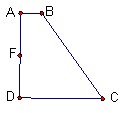
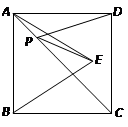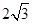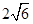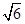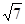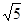设A,B表示两个集合,我们规定“A∩B”表示A与B的公共部分,并称之为A与B的交集.例如:若A={正数},B={整数},则A∩B={正整数}.如果A={矩形},B={菱形},则所对应的集合A∩B是
| A.{平行四边形} | B.{矩形} | C.{菱形} | D.{正方形} |
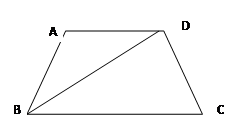
如图有一个含60°角的直角三角尺,沿其斜边和长直角边中点剪开后,不能拼成
的四边形是( )
| A.邻边不等的矩形 | B.等腰梯形 |
| C.有一角是锐角的菱形 | D.正方形 |
如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC,PF⊥CD,垂足分别为点
E,F,连接AP,EF,给出下列四个结论: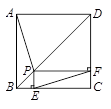
①AP =EF;②∠PFE=∠BAP;③PD= EC;④△APD一定是等腰三角形.其中正确的结论有
| A.1个 | B.2个 | C.3个 | D.4个 |
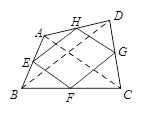
如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠DBC=30°,AD=5,则BC=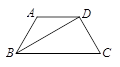
| A.5 | B.7.5 | C.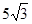 | D.10 |
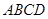 边长为4,
边长为4,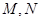 分别是
分别是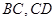 上的两个动点,当
上的两个动点,当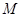 点在
点在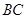 上运动时,保持
上运动时,保持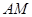 和
和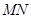 垂直,设
垂直,设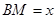 ,梯形
,梯形 的面积为
的面积为 ,下列结论
,下列结论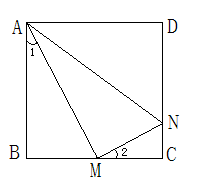
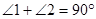
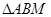 ∽
∽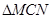
 的函数关系式为:
的函数关系式为: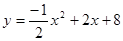
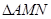

 。
。 ①②③
①②③  ①③④
①③④  ②③④
②③④  ②④
②④
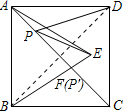
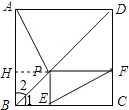
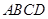 的面积为12,
的面积为12,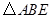 是等边三角形,点
是等边三角形,点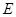 在正方形
在正方形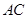 上有一点
上有一点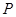 , 使
, 使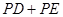 的和最小,则这个最小值为( )
的和最小,则这个最小值为( )