0 122432 122440 122446 122450 122456 122458 122462 122468 122470 122476 122482 122486 122488 122492 122498 122500 122506 122510 122512 122516 122518 122522 122524 122526 122527 122528 122530 122531 122532 122534 122536 122540 122542 122546 122548 122552 122558 122560 122566 122570 122572 122576 122582 122588 122590 122596 122600 122602 122608 122612 122618 122626 366461

 在同一直线上,
在同一直线上, ∥
∥ ,且
,且 ,
, ,求证:
,求证: ∥
∥ .
.

 与
与 全等吗?请说明理由;(4分)
全等吗?请说明理由;(4分) 的形状是 (2分)
的形状是 (2分)



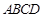 和四边形
和四边形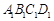 为例,分为以下四类:
为例,分为以下四类: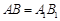 ,
, ,
,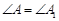 ,
,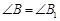 ,
,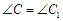 ;
;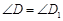 ;
;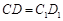 ,
,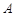 、
、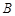 、
、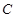 三点均在
三点均在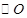 上,且
上,且 是等边三角形.
是等边三角形.
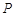 是
是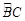 上一点,连接
上一点,连接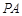 、
、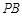 、
、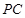 .探究
.探究 EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D。
EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D。


 的面积;
的面积; ),求y与t的关系式;是否存在某一时刻t,使四边形APQC的面积是
),求y与t的关系式;是否存在某一时刻t,使四边形APQC的面积是