已知函数
，当函数值y随x的增大而减小时，x的取值范围是（ ）
| A．x<1 | B．x>1 | C．x>－2 | D．－2<x<4 |
的图象向左平移2个单位，再向上平移1个单位，所得到的图象对应的二次函数表达式是（ ）
已知二次函数
（
）的图象如图所示，有下列结论：⑴abc>0；⑵a+b+c>0；⑶a-b+c<0；其中正确的结论有（ ）
| A．0个 | B．1个 | C．2个 | D．3个 |
二次函数
与y轴交点坐标为（ ）
| A．（0，1） | B．（0，2） | C．（0，-1） | D．（0，-2） |
抛物线
的顶点坐标为（ ）
| A．（2 ，5） | B．（-5 ，2） | C．（5 ，2） | D．（-5 ，-2） |
抛物线
的部分图象如图所示，要使
，则x的取值范围是
| A．-4<x<1 | B．-3<x<1 |
| C．x<-4或x>1 | D．x<-3或x>1 |
小明、小亮、小梅、小花四人共同探究代数式x2-4x+5的值的情况，他们作了如下分工：小明负责找值为1时的x值，小亮负责找值为0时的x值，小梅负责找最小值，小花负责找最大值。几分钟后，各自通报探究的结论，其中错误的是（ ）
| A．小明认为只有当x=2时，x2-4x+5的值为1； |
| B．小亮认为找不到实数x，使x2-4x+5的值为0； |
| C．小花发现当取大于2的实数时，x2-4x+5的值随x的增大而增大，因此认为没有最大值； |
| D．小梅发现x2-4x+5的值随x的变化而变化，因此认为没有最小值； |
抛物线y=ax2+bx+c的图角如图，则下列结论：①abc>0；②a+b+c=2；③a>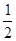
；④b<1．其中正确的结论是（ ）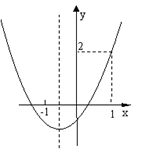
| A．①② | B．②④ | C．②③ | D．③④ |
把抛物线y=3x2向右平移一个单位，则所得抛物线的解析式为…………… ( )
| A．y=3(x+1)2 | B．y=3(x-1)2 | C．y=3x2+1 | D．y=3x2-1 |
已知二次函数
的图象如图所示，令
，则（ ）
| A．M＞0 | B．M＜0 |
| C．M＝0 | D．M的符号不能确定 |