生活中,在分析研究比赛成绩时经常要考虑不等关系.例如:一射击运动员在一次比赛中将进行10次射击,已知前7次射击共中61环,如果他要打破88环(每次射击以1到10的整数环计数)的记录,问第8次射击不能少于多少环?
我们可以按以下思路分析:
首先根据最后二次射击的总成绩可能出现的情况,来确定要打破88环的记录,第8次射击需要得到的成绩,并完成下表:
最后二次射击总成 绩 绩 | 第8次射击需得成绩 |
| 20环 | |
| 19环 | |
| 18环 | |
解:设第8次射击的成绩为x环,则可列出一个关于x的不等式:( )解得( )
所以第8次设计不能少于 ( )环
一手机经销商计划购进某品牌的A型、B型、C型三款手机共60部,每款手机至少要购进8部,且恰好用完购机款61000元.设购进A型手机x部,B型手机y部.三款手机的进价和预售价如下表:
| 手机型号 | A型 | B型 | C型 |
| 进 价(单位:元/部) | 900 | 1200 | 1100 |
| 预售价(单位:元/部) | 1200 | 1600 | 1300 |
(2)求出y与x之间的函数关系式;
(3)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润P(元)与x(部)的函数关系式;(注:预估利润P=预售总额-购机款-各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
(12分)“5·12”四川汶川大地震的灾情牵动全国人民的心,某市A、B两个蔬菜基地得知四川C、D两个灾民安置点分别急需蔬菜240吨和260吨的消息后,决定调运蔬菜支援灾区.已知A蔬菜基地有蔬菜200吨,B蔬菜基地有蔬菜300吨,现将这些蔬菜全部调往C、D两个灾民安置点.从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
| | C | D | 总计 |
| A | | | 200吨 |
| B | x吨 | | 300吨 |
| 总计 | 240吨 | 2 60吨 60吨 | 500吨 |
(2)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少
 元(
元( >0),其余线路的运费不变,试讨论总运费最小的调运方案.
>0),其余线路的运费不变,试讨论总运费最小的调运方案.(3)不
 等式与不等式组参考答案仅供参考
等式与不等式组参考答案仅供参考 . (12分)七年级(2)班有50名学生,老师安排每人制作一 件A型或B型的陶艺品,学校现有甲种制作材料36kg,乙种制作材料29kg,制作A、B两种型号的陶艺品用料情况如下表:
件A型或B型的陶艺品,学校现有甲种制作材料36kg,乙种制作材料29kg,制作A、B两种型号的陶艺品用料情况如下表:
| | 需甲种材料 | 需乙种材料 |
| 1件A型陶艺品 | 0.9kg | 0.3kg |
| 1件B型陶艺品 | 0.4kg | 1kg |
 件,
件, 求
求 的取值范围.
的取值范围.(2)请你根据学校现有材料,分别写出七年级(2)班制作A型和B型陶艺品的件数.
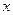 名老人,则这批牛奶共有多少盒?(用含
名老人,则这批牛奶共有多少盒?(用含


 ;并写出它的最小整数解.
;并写出它的最小整数解. 助设计出来?
助设计出来? 水厂处理相比较,10年节约资金多少万元?(注:企业处理污水的费用包括购买设备的资金和消耗费)
水厂处理相比较,10年节约资金多少万元?(注:企业处理污水的费用包括购买设备的资金和消耗费)