如图所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上，若∠1=35°，则∠2的度数为（　　）

一组数据：10、5、15、5、20，则这组数据的平均数和中位数分别是（　　）

方程=0的解为（　　）

下面四个几何体中，左视图是四边形的几何体共有（　　）

在网络上用“Google”搜索引擎搜索“中国梦”，能搜索到与之相关的结果个数约为45100000，这个数用科学记数法表示为

（　　）

在，，﹣2，﹣1这四个数中，最大的数是（　　）

在平面直角坐标系xOy中，一次函数y=2x+2的图象与x轴交于A，与y轴交于点C，点B的坐标为（a，0），（其中a＞0），直线l过动点M（0，m）（0＜m＜2），且与x轴平行，并与直线AC、BC分别相交于点D、E，P点在y轴上（P点异于C点）满足PE=CE，直线PD与x轴交于点Q，连接PA．

（1）写出A、C两点的坐标；

（2）当0＜m＜1时，若△PAQ是以P为顶点的倍边三角形（注：若△HNK满足HN=2HK，则称△HNK为以H为顶点的倍边三角形），求出m的值；

（3）当1＜m＜2时，是否存在实数m，使CD•AQ=PQ•DE？若能，求出m的值（用含a的代数式表示）；若不能，请说明理由．

在平面直角坐标系xOy中，已知点A（6，0），点B（0，6），动点C在以半径为3的⊙O上，连接OC，过O点作OD⊥OC，OD与⊙O相交于点D（其中点C、O、D按逆时针方向排列），连接AB．

（1）当OC∥AB时，∠BOC的度数为　45°或135°　；

（2）连接AC，BC，当点C在⊙O上运动到什么位置时，△ABC的面积最大？并求出△ABC的面积的最大值．

（3）连接AD，当OC∥AD时，

①求出点C的坐标；②直线BC是否为⊙O的切线？请作出判断，并说明理由．

用水平线和竖起线将平面分成若干个边长为1的小正方形格子，小正方形的顶点称为格点，以格点为顶点的多边形称为格点多边形．设格点多边形的面积为S，该多边形各边上的格点个数和为a，内部的格点个数为b，则S=a+b﹣1（史称“皮克公式”）．

小明认真研究了“皮克公式”，并受此启发对正三角开形网格中的类似问题进行探究：正三角形网格中每个小正三角形面积为1，小正三角形的顶点为格点，以格点为顶点的多边形称为格点多边形，下图是该正三角形格点中的两个多边形：

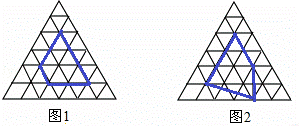
根据图中提供的信息填表：

则S与a、b之间的关系为S=　a+2（b﹣1）　（用含a、b的代数式表示）．

某饮料厂以300千克的A种果汁和240千克的B种果汁为原料，配制生产甲、乙两种新型饮料，已知每千克甲种饮料含0.6千克A种果汁，含0.3千克B种果汁；每千克乙种饮料含0.2千克A种果汁，含0.4千克B种果汁．饮料厂计划生产甲、乙两种新型饮料共650千克，设该厂生产甲种饮料x（千克）．

（1）列出满足题意的关于x的不等式组，并求出x的取值范围；

（2）已知该饮料厂的甲种饮料销售价是每1千克3元，乙种饮料销售价是每1千克4元，那么该饮料厂生产甲、乙两种饮料各多少千克，才能使得这批饮料销售总金额最大？