（本小题满分10分）
学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化.
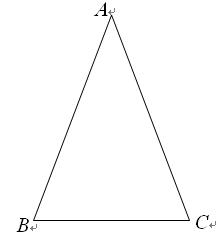
类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）.如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=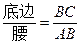
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义，解下列问题：
（1）sad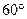
的值为（ ）
（2）对于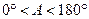
，∠A的正对值sad A的取值范围是 .
（3）已知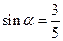
，其中
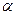为锐角，试求sad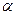的值.
学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化.
类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）.如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=
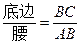.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述对角的正对定义，解下列问题：
（1）sad
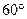的值为（ ）A． | B．1 | C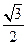． | D．2 |
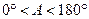，∠A的正对值sad A的取值范围是 .（3）已知
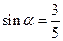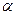，其中为锐角，试求sad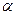的值. 
时，求线段
的长；
计算
的结果是……………………………………………………（ ）
（
的结果是……………………………………………………（ ）（
A． ； | B． ； | C． ； | D． ． |
下列方程中，有实数根的方程是 ……………………………（ ）
A． ； | B． ； | C． ； | D． ． |
在平面直角坐标系内，把点
（－3，1）向右平移一个单位，则得到的对应点
的坐标是（ ）
（－3，1）向右平移一个单位，则得到的对应点的坐标是（ ）| A．（－3，2）； | B．（－3，0）； | C．（－4，1）； | D．（－2，1）． |
在
中，点
、
、
分别在
、
、
上，且
，
，则下列三种说法：
①如果
，那么四边形
是矩形；
②如果
平分
，那么四边形是菱形；
③如果
且
，那么四边形是菱形．
其中正确的有 ………………………………………（ ）
中，点、、分别在、、上，且，，则下列三种说法：①如果
，那么四边形是矩形； ②如果
平分，那么四边形是菱形；③如果
且，那么四边形是菱形．其中正确的有 ………………………………………（ ）
| A．3个； | B．2个； | C．1个； | D．0个． |
在
中，
，且两边长分别为4
和5，若以点
为圆心，3为半径作⊙，以点
为圆心，2为半径作⊙，则⊙和⊙位置关系是………（ ）
0 112404 112412 112418 112422 112428 112430 112434 112440 112442 112448 112454 112458 112460 112464 112470 112472 112478 112482 112484 112488 112490 112494 112496 112498 112499 112500 112502 112503 112504 112506 112508 112512 112514 112518 112520 112524 112530 112532 112538 112542 112544 112548 112554 112560 112562 112568 112572 112574 112580 112584 112590 112598 366461
中，，且两边长分别为4和5，若以点为圆心，3为半径作⊙，以点为圆心，2为半径作⊙，则⊙和⊙位置关系是………（ ）| A．只有外切一种情况； | B．只有外离一种情况； |
| C．有相交或外切两种情况； | D．有外离或外切两种情况． |
．
，
，则
．
．