、阅读下列材料并填空。平面上有n个点(n≥2)且任意三个点不在同一条直线上,过这些点作直线,一共能作出多少条不同的直线?
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线……
②归纳:考察点的个数和可连成直线的条数 发现:如下表
发现:如下表
③推理:平面上有n个点,两点确定一条直线。取第一个点A有n种取法,取第二个点B有(n-1)种取法,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,故应除以2;即
④结论:
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1)分析:
当仅有3个点时,可作出 个三角形;
当仅有4个点时,可作出 个三角形;
当仅有5个点时,可作出 个三角形;
……
(2)归纳:考察点的个数n和可作出的三角形的个数 ,发现:(填下表)
,发现:(填下表)
(3)推理:
(4)结论:
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线……
②归纳:考察点的个数和可连成直线的条数
 发现:如下表
发现:如下表| 点的个数 | 可作出直线条数 |
| 2 | 1= |
| 3 | 3=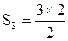 |
| 4 | 6= |
| 5 | 10= |
| …… | …… |
| n |  |

④结论:

试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1)分析:
当仅有3个点时,可作出 个三角形;
当仅有4个点时,可作出 个三角形;
当仅有5个点时,可作出 个三角形;
……
(2)归纳:考察点的个数n和可作出的三角形的个数
 ,发现:(填下表)
,发现:(填下表)| 点的个数 | 可连成三角形个数 |
| 3 | |
| 4 | |
| 5 | |
| …… | |
| n | |
(3)推理:
(4)结论:
一3的绝对值是( )
| A.3 | B.±3 | C. 3 | D.± |
2004年聊城市的国民生产总值为1012亿元,用科学记数法表示正确的是( )
A.1012×10 元 元 | B.1.012× 元 元 | C.1.0× 元. 元. | D.1.012× 元. 元. |
下列各式计算正确的是( )
A. . . | B. | C. | D. 。 。 |
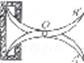
如图,将两根钢条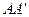 、
、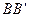 的中点O连在一起,使
的中点O连在一起,使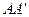 、
、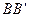 可以绕着点0自由转动,就做成了一个测量工件,则
可以绕着点0自由转动,就做成了一个测量工件,则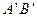 的长等于内槽宽AB,那么判定△AOB
的长等于内槽宽AB,那么判定△AOB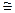 △
△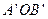 的理由是( )
的理由是( )
0 112207 112215 112221 112225 112231 112233 112237 112243 112245 112251 112257 112261 112263 112267 112273 112275 112281 112285 112287 112291 112293 112297 112299 112301 112302 112303 112305 112306 112307 112309 112311 112315 112317 112321 112323 112327 112333 112335 112341 112345 112347 112351 112357 112363 112365 112371 112375 112377 112383 112387 112393 112401 366461
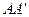 、
、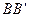 的中点O连在一起,使
的中点O连在一起,使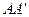 、
、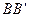 可以绕着点0自由转动,就做成了一个测量工件,则
可以绕着点0自由转动,就做成了一个测量工件,则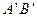 的长等于内槽宽AB,那么判定△AOB
的长等于内槽宽AB,那么判定△AOB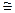 △
△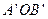 的理由是( )
的理由是( )
| A.边角边 | B.角边角 | C.边边边 | D.角角边 |
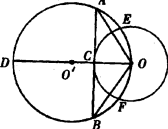
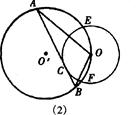
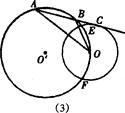
 的中点,CD是⊙O的直径,过C点的直线
的中点,CD是⊙O的直径,过C点的直线 交AB所在直线于点E,交⊙O于点F。
交AB所在直线于点E,交⊙O于点F。 与
与 的数量关系,并写出结论;
的数量关系,并写出结论;

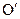 经过半径为r的⊙O的圆心,⊙O与⊙
经过半径为r的⊙O的圆心,⊙O与⊙