题目内容

在半径为2的圆中有一个内接正方形，现随机地往圆内投一粒米，落在正方形内的概率为________．（注：π取3）

$\text{[math]}$
分析：根据已知首先求出圆的面积以及正方形的边长，进而得出正方形的面积，即可得出落在正方形内的概率．
解答：

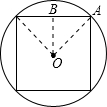解：∵在半径为2的圆中有一个内接正方形，现随机地往圆内投一粒米，
∴圆的面积为：π×2²=4π≈12．
∵正方形的边长为：AB²+BO²=AO²，
∴2AB²=4，
∴AB= $\text{[math]}$ ，
正方形边长为：2 $\text{[math]}$ ，
∴正方形面积为：8，
∴落在正方形内的概率为：8÷12= $\text{[math]}$ ．
故答案为： $\text{[math]}$ ．
点评：此题主要考查了几何概率、圆的面积求法以及正方形的特殊性质，求出两图形的面积是解决问题的关键．