题目内容
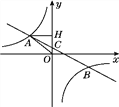
【题目】在平面直角坐标系xOy中,直线y=2x+l与双曲线y=![]() 的一个交点为A(m,-3).
的一个交点为A(m,-3).
(1)求双曲线的表达式;
(2)过动点P(n,0)(n<0)且垂直于x轴的直线与直线y=2x+l和双曲线y=![]() 的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
【答案】(1)y=![]() ;(2)-2<n<0.
;(2)-2<n<0.
【解析】试题分析:(1)根据点A的纵坐标利用一次函数图象上点的坐标特征,可求出点A的坐标,根据点A的坐标利用待定系数法,即可求出双曲线的表达式;
(2)依照题意画出函数图象,根据两函数图象的上下位置关系,即可找出n的取值范围.
试题解析:
(1)当y=2x+1=-3时,x=-2,
∴点A的坐标为(-2,-3),
将点A(-2,-3)代入y=![]() 中,
中,
-3=![]() ,解得:k=6,
,解得:k=6,
∴双曲线的表达式为y=![]() .
.
(2)依照题意,画出图形,如图所示.

观察函数图象,可知:当-2<x<0时,直线y=2x+1在双曲线y=![]() 的上方,
的上方,
∴当点B位于点C上方时,n的取值范围为-2<n<0.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
【题目】2019年中国快递行业竞争激烈,为了占据市场赢得消费者青睐,某快递公司出台了市内快件收费标准:凡是重庆市内的快递统一收取基础费用8元,快递质量不超过10kg,不加收费用;快递质量大于10kg,则超过10g的部分按0.3元/kg收费.
(1)某同学需要将重量为x(x>10)千克的书籍在重庆市内同城快递回家,则该同学需付快递费用y元,用含x的代数式表示y.
(2)因国庆阅兵需要将一些纪念品从重庆寄往相距1800千米的北京,该快递公司获得这项任务后,调整了市外快件收费标准,收费标准如下表.已知纪念品重量为a千克,则纪念品从重庆运往北京的快递费为多少元?(用含a的代数式表示w)
价格表 | |
重量费 | 距离费 |
不超过10kg统一收取5元 | 0.01元/km |
超过10kg不超过50kg的部分0.2元/kg | |
超过50kg部分0.4元/kg | |
(注:快递费=重量费+距离费) | |