题目内容
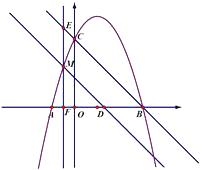
【题目】如图,在平面直角坐标系中,直线![]() 交x轴于点A,交y轴于点B,交直线
交x轴于点A,交y轴于点B,交直线![]() 于点C,点D与点B关于x轴对称,连接AD交直线
于点C,点D与点B关于x轴对称,连接AD交直线![]() 于点E.
于点E.
![]() 填空:
填空:![]() ______.
______.
![]() 求直线AD的解析式;
求直线AD的解析式;
![]() 在x轴上存在一点P,则
在x轴上存在一点P,则![]() 的和最小为______;
的和最小为______;![]() 直接填空即可
直接填空即可![]()
![]() 当
当![]() 时,点Q为y轴上的一个动点,使得
时,点Q为y轴上的一个动点,使得![]() 为等腰直角三角形,求点Q的坐标.
为等腰直角三角形,求点Q的坐标.

【答案】(1)12;(2)![]() ;(3)
;(3)![]() ;(4)点Q的坐标为
;(4)点Q的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
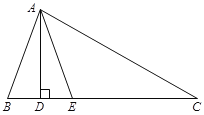
![]() 分别计算A、B、D三点的坐标,可得OA和BD的长,根据三角形面积公式可得结论;
分别计算A、B、D三点的坐标,可得OA和BD的长,根据三角形面积公式可得结论;
![]() 利用待定系数法可得直线AD的解析式;
利用待定系数法可得直线AD的解析式;
![]() 根据轴对称的最短路径先确认P的位置:连接BE交x轴于P,此时,
根据轴对称的最短路径先确认P的位置:连接BE交x轴于P,此时,![]() 最小,即是BE的长,利用勾股定理可计算BE的长,最后将其配方后,根据二次函数的最值可得结论;
最小,即是BE的长,利用勾股定理可计算BE的长,最后将其配方后,根据二次函数的最值可得结论;
![]() 存在三种情况:分别以Q、E、C三个顶点为直角顶点,画图可得Q的坐标.
存在三种情况:分别以Q、E、C三个顶点为直角顶点,画图可得Q的坐标.
![]() 如图1,
如图1,![]() 直线
直线![]() 交x轴于点A,交y轴于点B,
交x轴于点A,交y轴于点B,
令![]() ,
,![]() ,
,
![]() ,
,
令![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 点D与点B关于x轴对称,
点D与点B关于x轴对称,
![]() ,
,
![]() ,
,
故答案为:12;
![]() 如图1,设直线AD的解析式为
如图1,设直线AD的解析式为![]() ,由
,由![]() 知,
知,![]() ,
,![]() ,
,
![]() ,
,
 ,
,
![]() 直线AD的解析式为
直线AD的解析式为![]() ;
;
![]() 如图2,由
如图2,由![]() 知,直线AD的解析式为
知,直线AD的解析式为![]() ,
,
![]() 直线CE:
直线CE:![]() ,
,
![]() ,
,
![]() 点D与点B关于x轴对称,
点D与点B关于x轴对称,
![]() 连接BE交x轴于P,
连接BE交x轴于P,
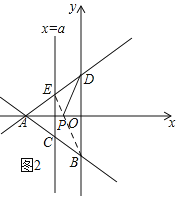
此时,![]() 最小,最小值为BE,
最小,最小值为BE,
![]() ,
,
![]() 的最小值是
的最小值是![]() ,
,
则![]() 的和最小为
的和最小为![]() ;
;
故答案为:![]() ;
;
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
设![]() ,
,![]() ,
,
![]() 为等腰直角三角形时,存在以下三种情况:
为等腰直角三角形时,存在以下三种情况:
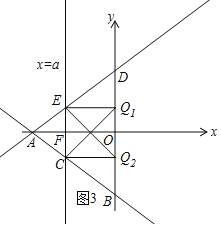
![]() 当E为直角顶点时,如图3,
当E为直角顶点时,如图3,
![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
![]() ;
;
![]() 当C为直角顶点时,如图3,同理得
当C为直角顶点时,如图3,同理得![]() ;
;
![]() 当Q为直角顶点时,如图4,
当Q为直角顶点时,如图4,
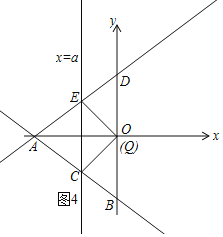
此时Q与O重合,![]()
综上,点Q的坐标为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目