题目内容
 如图,直线y=3x+3交坐标轴于A,B,点C在双曲线y=
如图,直线y=3x+3交坐标轴于A,B,点C在双曲线y= (x<0)上,且BC⊥AB,连接AC交双曲线于D,若D恰好为AC的中点,则k的值为________.
(x<0)上,且BC⊥AB,连接AC交双曲线于D,若D恰好为AC的中点,则k的值为________.
-4
分析:对于直线y=3x+3,分别令x与y为0求出对应y与x的值,确定出A与B坐标,根据BC与AB垂直,利用两直线垂直时斜率的乘积为-1求出BC的斜率,进而确定出直线BC的解析式,与反比例函数解析式联立表示出C坐标,再利用线段中点坐标公式表示出D坐标,代入反比例解析式中列出关于k的方程,求出方程的解即可得到k的值,
解答:对于直线y=3x+3,
令x=0,得到y=3;令y=0,得到x=-1,
∴A(0,3),B(-1,0),
∴直线BC解析式为y=-(x+1)=-x-1,
y=-x-1与反比例解析式联立消去y得: =-x-1,
=-x-1,
去分母得:x2+x+k=0,
解得:x= (舍去),或x=
(舍去),或x= ,
,
∴y= -1,即C(
-1,即C( ,
, -1),
-1),
∵D为AC中点,
∴D( ,
, +1),
+1),
将D坐标代入反比例解析式得: •(
•( +1)=k,
+1)=k,
解得:k=-4.
故答案为:-4
点评:此题考查了一次函数与反比例函数的交点问题,涉及的知识有:线段中点坐标公式,两直线垂直时斜率满足的关系,一次函数与坐标轴的交点,以及坐标与图形性质,是一道中档题.
分析:对于直线y=3x+3,分别令x与y为0求出对应y与x的值,确定出A与B坐标,根据BC与AB垂直,利用两直线垂直时斜率的乘积为-1求出BC的斜率,进而确定出直线BC的解析式,与反比例函数解析式联立表示出C坐标,再利用线段中点坐标公式表示出D坐标,代入反比例解析式中列出关于k的方程,求出方程的解即可得到k的值,
解答:对于直线y=3x+3,
令x=0,得到y=3;令y=0,得到x=-1,
∴A(0,3),B(-1,0),
∴直线BC解析式为y=-(x+1)=-x-1,
y=-x-1与反比例解析式联立消去y得:
 =-x-1,
=-x-1,去分母得:x2+x+k=0,
解得:x=
 (舍去),或x=
(舍去),或x= ,
,∴y=
 -1,即C(
-1,即C( ,
, -1),
-1),∵D为AC中点,
∴D(
 ,
, +1),
+1),将D坐标代入反比例解析式得:
 •(
•( +1)=k,
+1)=k,解得:k=-4.
故答案为:-4
点评:此题考查了一次函数与反比例函数的交点问题,涉及的知识有:线段中点坐标公式,两直线垂直时斜率满足的关系,一次函数与坐标轴的交点,以及坐标与图形性质,是一道中档题.

练习册系列答案
相关题目
 如图:直线y=-3x+6与y轴交于点A,与直线y=2x+1交于点B,且直线y=2x+1与x轴交于点C,则△ABC的面积为
如图:直线y=-3x+6与y轴交于点A,与直线y=2x+1交于点B,且直线y=2x+1与x轴交于点C,则△ABC的面积为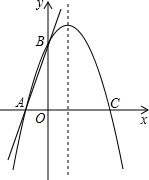 如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).
如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0). (2012•双柏县二模)如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).
(2012•双柏县二模)如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0). ,0).
,0).