题目内容
在直角三角形中，三个内角度数的比为1：2：3，若斜边为2，则两直角边的和为
1+
．
| 3 |
1+
．
．| 3 |
分析：由三角形内角和定理求得三角形的三个内角分别是30°、60°、90°．由30度角所对的直角边是斜边的一半求得一直角边的长度，然后由勾股定理求得另一直角边的长度．
解答：
解：如图，在直角△ABC中，∠A：∠B：∠C=1：2：3，AB=2，
∵∠A+∠B+∠C=180°，
∴∠A=30°，∠B=60°，∠C=90°，
∴BC=
AB=1，
∴BC=
=
，
∴AC+BC=1+
．
故答案是：1+
．
解：如图，在直角△ABC中，∠A：∠B：∠C=1：2：3，AB=2，∵∠A+∠B+∠C=180°，
∴∠A=30°，∠B=60°，∠C=90°，
∴BC=
| 1 |
| 2 |
∴BC=
| AB2-AC2 |
| 3 |
∴AC+BC=1+
| 3 |
故答案是：1+
| 3 |
点评：本题考查了含30度角的直角三角形，勾股定理．注意勾股定理适合于直角三角形中．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
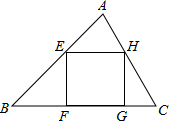某课题学习小组在一次活动中对三角形的内接正方形的有关问题进行了探讨：