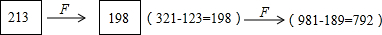题目内容
定义[p，q]为一次函数y=px+q的特征数．若特征数是[2，k-2]的一次函数为正比例函数，则k的值是______．
根据题意，特征数是[2，k-2]的一次函数表达式为：y=2x+（k-2）．
因为此一次函数为正比例函数，所以k-2=0，
解得：k=2．
故填2．
因为此一次函数为正比例函数，所以k-2=0，
解得：k=2．
故填2．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
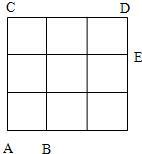15、宋朝时，中国象棋就已经风靡于全国，中国象棋规定马步为：“
、
”形的对角线（即一次对角线为一步），现定义：在棋盘上从点A到点B，马走的最少步称为A与B的“马步距离”，记作dA-＞B．在图中画出了中国象棋的一部分，上面标有A，B，C，D，E共5个点，则在dA-＞B，dA-＞C，dA-＞D，dA-＞E中小的是
