Question

【题目】在△ABC中,∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.

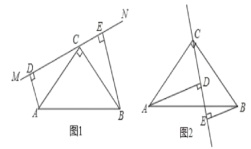
(1)当直线MN绕点C旋转到图1的位置时，△ADC和△CEB全等吗?请说明理由；

(2)聪明的小亮发现，当直线MN绕点C旋转到图1的位置时，可得DE=AD+BE，请你说明其中的理由；

(3)小亮将直线MN绕点C旋转到图2的位置，发现DE、AD、BE之间存在着一个新的数量关系，请直接写出这一数量关系。

Answer 1

【答案】（1）全等，理由见解析；（2）见解析；（3）DE=ADBE.理由见解析

【解析】

（1）根据同角的余角相等得到∠ACD=∠BCE，证明△ADC≌△CEB即可；

（2）根据全等三角形的性质得到BE=CD，CE=AD，结合图形得到结论；

（3）与（1）的证明方法类似，证明△ADC≌△CEB即可．

(1)△ADC≌△CEB.

理由如下：∵∠ACB=90°，

∴∠ACD+∠BCE=90°，

∵BE⊥MN，

∴∠CBE+∠BCE=90°，

∴∠ACD=∠BCE，

在△ADC和△CEB中，

，

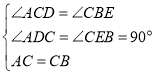∴△ADC≌△CEB；

(2)∵△ADC≌△CEB，

∴BE=CD，CE=AD，

∴DE=CE+CD=AD+BE；

(3)DE=ADBE.

证明：∵∠ACB=90°，

∴∠ACD+∠BCE=90°，

∵AD⊥MN，

∴∠ACD+∠DAC=90°，

∴∠DAC=∠BCE，

在△ADC和△CEB中，

，

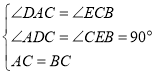∴△ADC≌△CEB，

∴AD=CE，CD=BE，

∴DE=CECD=ADBE.