题目内容
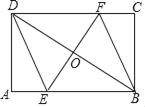
【题目】(1)如图1,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG。求证:①∠BEA =∠G,② EF=FG。
(2)如图2,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长。

【答案】(1)①见解析②见解析(2)![]()
【解析】
(1)在△ABE和△ADG中,根据SAS得出△ABE≌△ADG则∠BEA=∠G.然后在△FAE和△GAF中通过SAS证明得出△FAE≌△GAF,则EF=FG.
(2)过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM.连接AE、EN.在△ABM和△ACE中,通过SAS证明得出△ABM≌△ACE, AM=AE, ∠BAM+∠CAN=45°. 在△MAN和△EAN中,通过SAS证明得出△MAN≌△EAN, MN=EN. Rt△ENC中,由勾股定理,得EN2=EC2+NC2得出最终结果.
(1)证明:在正方形ABCD中,∠ABE=∠ADG,AD=AB,
在△ABE和△ADG中,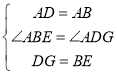 ,
,
∴△ABE≌△ADG(SAS),∠BEA=∠G
∴∠BAE=∠DAG,AE=AG,
又∠BAD=90°,
∴∠EAG=90°,∠FAG=45°
在△FAE和△GAF中,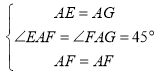 ,
,
∴△FAE≌△GAF(SAS),
∴EF=FG
(2)
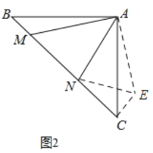
解:如图,过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM.连接AE、EN.
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°.
∵CE⊥BC,
∴∠ACE=∠B=45°.
在△ABM和△ACE中,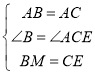 ,
,
∴△ABM≌△ACE(SAS).
∴AM=AE,∠BAM=∠CAE.
∵∠BAC=90°,∠MAN=45°,
∴∠BAM+∠CAN=45°.
于是,由∠BAM=∠CAE,得∠MAN=∠EAN=45°.
在△MAN和△EAN中,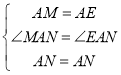 ,
,
∴△MAN≌△EAN(SAS).
∴MN=EN.
在Rt△ENC中,由勾股定理,得EN2=EC2+NC2.
∴MN2=BM2+NC2.
∵BM=1,CN=3,
∴MN2=12+32,
∴MN=![]() .
.

【题目】在学校组织的“学习强国”知识竞赛中,每班参加比赛的人数相同,成绩分为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级其中相应等级的得分依次记为
四个等级其中相应等级的得分依次记为![]() 分,
分,![]() 分,
分,![]() 分和
分和![]() 分.年级组长张老师将
分.年级组长张老师将![]() 班和
班和![]() 班的成绩进行整理并绘制成如下的统计图:
班的成绩进行整理并绘制成如下的统计图:
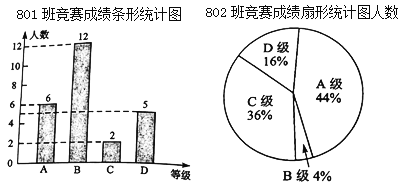
(1)在本次竞赛中,![]() 班
班![]() 级的人数有多少。
级的人数有多少。
(2)请你将下面的表格补充完整:
成绩 班级 | 平均数(分) | 中位数 (分) | 众数 (分) | B级及以上人数 |
|
|
|
| |
|
|
|
(3)结合以上统计量,请你从不同角度对这次竞赛成绩的结果进行分析(写出两条)