题目内容
下列各数: ,0,
,0,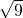 ,0.2
,0.2 ,cos60°,
,cos60°,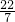 ,0.3000333…,1-
,0.3000333…,1- 中无理数个数为
中无理数个数为
- A.2个
- B.3个
- C.4个
- D.5个
A
分析:无理数是无限不循环小数,其中有开方开不尽的数,根据无理数的定义以及无理数的常见形式判断并选择即可求解.
解答:根据无理数和有理数的概念可得,
0,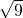 ,0.2
,0.2 ,cos60°,
,cos60°,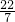 ,0.3000333…是有理数(其中0.3000333…是无限循环小数);
,0.3000333…是有理数(其中0.3000333…是无限循环小数);
 ,1-
,1- 是无理数,共2个.
是无理数,共2个.
故选A.
点评:此题主要考查了无理数的定义,其中利用了:
(1)有理数都可以化为小数,其中整数可以看作小数点后面是零的小数,例如5=5.0;分数都可以化为有限小数或无限循环小数.
(2)无理数是无限不循环小数,其中有开方开不尽的数.
(3)有限小数和无限循环小数都可以化为分数,也就是说,一切有理数都可以用分数来表示;而无限不环小数不能化为分数,它是无理数.
分析:无理数是无限不循环小数,其中有开方开不尽的数,根据无理数的定义以及无理数的常见形式判断并选择即可求解.
解答:根据无理数和有理数的概念可得,
0,
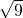 ,0.2
,0.2 ,cos60°,
,cos60°,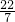 ,0.3000333…是有理数(其中0.3000333…是无限循环小数);
,0.3000333…是有理数(其中0.3000333…是无限循环小数); ,1-
,1- 是无理数,共2个.
是无理数,共2个.故选A.
点评:此题主要考查了无理数的定义,其中利用了:
(1)有理数都可以化为小数,其中整数可以看作小数点后面是零的小数,例如5=5.0;分数都可以化为有限小数或无限循环小数.
(2)无理数是无限不循环小数,其中有开方开不尽的数.
(3)有限小数和无限循环小数都可以化为分数,也就是说,一切有理数都可以用分数来表示;而无限不环小数不能化为分数,它是无理数.

练习册系列答案
相关题目