题目内容
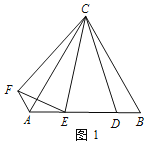
【题目】在△ABC中,AC=BC,射线AP交边BC于点E,点D是射线AP上一点,连接BD、CD .
(1)如图1,当∠CAB=45°,∠BDP=90°时,请直接写出DA与DB、DC之间满足的数量关系为: .
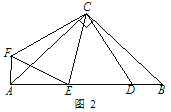
(2)如图2,当∠CAB=30°,∠BDP=60°时,试猜想:DA与DB、DC之间具有怎样的数量关系?并说明理由.
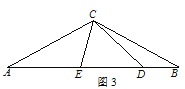
(3)如图3,当∠ACB=![]() ,∠BDP=
,∠BDP=![]() ,若
,若![]() 与
与![]() 之间满足
之间满足![]() ,则DA与DB、DC之间的数量关系为 .(请直接写出结论)
,则DA与DB、DC之间的数量关系为 .(请直接写出结论)

【答案】(1)![]() ;(2)
;(2)![]() ,证明见解析;(3)AD=BD+CD·Sin
,证明见解析;(3)AD=BD+CD·Sin![]()
【解析】(1)结论:AD=BD+![]() CD.只要证明△ACM≌△BCD,推出CM=CD,AM=BD,推出△CDM是等腰直角三角形,推出DM=
CD.只要证明△ACM≌△BCD,推出CM=CD,AM=BD,推出△CDM是等腰直角三角形,推出DM=![]() CD,可得AD=AM+DM=BD+
CD,可得AD=AM+DM=BD+![]() CD;
CD;
(2)如图2中,结论∴AD=BD+![]() CD.只要证明△ACM≌△BCD,推出CM=CD,AM=BD,作CH⊥DM于H,则MH=DH=CDcos30°=
CD.只要证明△ACM≌△BCD,推出CM=CD,AM=BD,作CH⊥DM于H,则MH=DH=CDcos30°=![]() CD,推出DM=
CD,推出DM=![]() CD,可得AD=AM+DM=BD+
CD,可得AD=AM+DM=BD+![]() CD;
CD;
(3)如图3中,结论:AD=BD+2CDcosα.证明方法类似.
(1)结论:AD=BD+![]() CD.
CD.
理由:如图1中,作CM⊥CD交AD于M.
∵∠ACE=∠BDE=90°,∠AEC=∠BED,
∴∠CAM=∠CBD,
∵∠ACB=∠MCD=90°,
∴∠ACM=∠BCD,
∵AC=CB,
∴△ACM≌△BCD,
∴CM=CD,AM=BD,
∴△CDM是等腰直角三角形,
∴DM=![]() CD,
CD,
∴AD=AM+DM=BD+![]() CD.
CD.
故答案为:AD=BD+![]() CD.
CD.
(2)如图2中,结论∴AD=BD+![]() CD.
CD.
理由:如图2中,作∠DCM=∠ACB交AD于M.
∵∠ACE=∠BDE=120°,∠AEC=∠BED,
∴∠CAM=∠CBD,
∵∠ACB=∠MCD,
∴∠ACM=∠BCD,
∵AC=CB,
∴△ACM≌△BCD,
∴CM=CD,AM=BD,
作CH⊥DM于H,则MH=DH=CDcos30°=![]() CD,
CD,
∴DM=![]() CD,
CD,
∴AD=AM+DM=BD+![]() CD;
CD;
(3)如图3中,结论:AD=BD+2CDcosα.
理由:如图3中,作∠DCM=∠ACB交AD于M.
∵∠ACE=∠BDE,∠AEC=∠BED,
∴∠CAM=∠CBD,
∵∠ACB=∠MCD,
∴∠ACM=∠BCD,
∵AC=CB,
∴△ACM≌△BCD,
∴CM=CD,AM=BD,
作CH⊥DM于H,则MH=DH=CDcosα,
∴DM=2CDcosα,
∴AD=AM+DM=BD+2CDcosα.
故答案为:AD=BD+2CDcosα.