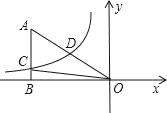
题目内容
【题目】如图,在直角坐标系中,直线![]() 与
与![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,
,![]() 是直线
是直线![]() 上一动点,且在点
上一动点,且在点![]() 的上方,设点
的上方,设点![]() .
.

(1)当四边形![]() 的面积为38时,求点
的面积为38时,求点![]() 的坐标,此时在
的坐标,此时在![]() 轴上有一点
轴上有一点![]() ,在
,在![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 最大,求出
最大,求出![]() 的最大值以及此时点
的最大值以及此时点![]() 坐标;
坐标;
(2)在第(1)问条件下,直线![]() 左右平移,平移的距离为
左右平移,平移的距离为![]() . 平移后直线上点
. 平移后直线上点![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]() 、点
、点![]() ,当
,当![]() 为等腰三角形时,直接写出
为等腰三角形时,直接写出![]() 的值.
的值.
【答案】(1)点D的坐标为(﹣2,10), 点M的坐标为(0,![]() )时,|ME﹣MD|取最大值2
)时,|ME﹣MD|取最大值2![]() ;(2) 当△A′B′D为等腰三角形时,t的值为﹣2﹣4
;(2) 当△A′B′D为等腰三角形时,t的值为﹣2﹣4![]() 、4、﹣2+4
、4、﹣2+4![]() 或9
或9
【解析】
(1)将x=-2代入直线AB解析式中即可求出点C的坐标,利用分割图形求面积法结合四边形AOBD的面积为38即可得出关于m的一元一次方程,解之即可得出m值,在x轴负半轴上找出点E关于y轴对称的点E′(-8,0),连接E′D并延长交y轴于点M,连接DM,根据三角形三边关系即可得出此时|ME-MD|最大,最大值为线段DE′的长度,由点D、E′的坐标利用待定系数法即可求出直线DE′的解析式,将x=0代入其中即可得出此时点M的坐标,再根据两点间的距离公式求出线段DE′的长度即可;
(2)根据平移的性质找出平移后点A′、B′的坐标,结合点D的坐标利用两点间的距离公式即可找出B′D、A′B′、A′D的长度,再根据等腰三角形的性质即可得出关于t的方程,解之即可得出t值,此题得解.
(1)当x=﹣2时,y=![]() ,
,
∴C(﹣2,![]() ),
),
∴S四边形AOBD=S△ABD+S△AOB=![]() CD(xA﹣xB)+
CD(xA﹣xB)+![]() OAOB=3m+8=38,
OAOB=3m+8=38,
解得:m=10,
∴当四边形AOBD的面积为38时,点D的坐标为(﹣2,10).
在x轴负半轴上找出点E关于y轴对称的点E′(﹣8,0),连接E′D并延长交y轴于点M,连接DM,此时|ME﹣MD|最大,最大值为线段DE′的长度,如图1所示.
DE′=![]() .
.
设直线DE′的解析式为y=kx+b(k≠0),
将D(﹣2,10)、E′(﹣8,0)代入y=kx+b,
![]() ,解得:
,解得: ,
,
∴直线DE′的解析式为y=![]() x+
x+![]() ,
,
∴点M的坐标为(0,![]() ).
).
故当点M的坐标为(0,![]() )时,|ME﹣MD|取最大值2
)时,|ME﹣MD|取最大值2![]() .
.
(2)∵A(0,8),B(﹣6,0),
∴点A′的坐标为(t,8),点B′的坐标为(t﹣6,0),
∵点D(﹣2,10),
∴B′D=![]() ,
,
A′B′=![]() =10,A′D=
=10,A′D=![]() .
.
△A′B′D为等腰三角形分三种情况:
①当B′D=A′D时,有![]() =
=![]() ,
,
解得:t=9;
②当B′D=A′B′时,有![]() =10,
=10,
解得:t=4;
③当A′B′=A′D时,有10=![]() ,
,
解得:t1=﹣2﹣4![]() (舍去),t2=﹣2+4
(舍去),t2=﹣2+4![]() .
.
综上所述:当△A′B′D为等腰三角形时,t的值为﹣2﹣4![]() 、4、﹣2+4
、4、﹣2+4![]() 或9.
或9.


 名校课堂系列答案
名校课堂系列答案【题目】有这样一个问题:
探究函数![]() 的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
(1)填表
| … |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | . . . |
| … | 3 | 2 |
|
| . . . |
(2)根据(1)中的结果,请在所给坐标系中画出函数![]() 的图象;
的图象;