题目内容
 在如图的方格纸中,每个小方格都是边长为1的正方形,点A、B、C、D是方格纸中的四个格点(即正方形的顶点),图中阴影部分是将四边形ABCD的四边中点连结起来而得到的图形,若将一个骰子投到这个方格纸中,则投到阴影部分的概率是
在如图的方格纸中,每个小方格都是边长为1的正方形,点A、B、C、D是方格纸中的四个格点(即正方形的顶点),图中阴影部分是将四边形ABCD的四边中点连结起来而得到的图形,若将一个骰子投到这个方格纸中,则投到阴影部分的概率是考点:几何概率
专题:
分析:首先求出阴影部分面积,利用阴影部分面积除以总面积,进而求出投到阴影部分的概率即可.
解答:解:如图所示:∵点A、B、C、D是方格纸中的四个格点(即正方形的顶点),图中阴影部分是将四边形ABCD的四边中点连结起来而得到的图形,
∴EH=
BD=2,EF=
AC=2,
∴四边形EFGH部分面积为:2×2=4,
∴投到阴影部分的概率是:
=
.
故答案为:
.
∴EH=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形EFGH部分面积为:2×2=4,
∴投到阴影部分的概率是:
| 4 |
| 16 |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查了几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
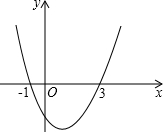 二次函数y=ax2+bx+c的图象如图所示,则下列说法中正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列说法中正确的是( )| A、ac>0 |
| B、4a+2b+c>0 |
| C、当x>1时,y随x的增大而减小 |
| D、a+b<m(am+b)(m≠1) |
为了解决迫在眉睫的环境问题,中国2013年预算案显示,中央和地方政府2013年将向节能和环境保护相关领域投入约32860000万元,将大力改善发电站的电力供应结构.近似数32860000用科学记数法可表示为( )
| A、3.286×105 |
| B、3.286×106 |
| C、3.286×107 |
| D、3.286×108 |
以数形结合的观点解题,方程x2+x-1=0的实根可看成函数y=x2与函数y=1-x的图象交点的横坐标,也可以看成函数y=x+1与函数y=
的图象交点的横坐标,那么用此方法可推断方程x3+x-1=0的一个实根x的所在范围是( )
| 1 |
| x |
A、-
| ||
B、0<x<
| ||
C、
| ||
D、1<x<
|
 九年级(1)班和(2)班各选派了七位学生参加一次科普知识竞赛,他们的成绩分别如下表:
九年级(1)班和(2)班各选派了七位学生参加一次科普知识竞赛,他们的成绩分别如下表: