题目内容
12、如果对任意实数x，等式：（1-2x）10=a0+a1x+a2x2+a3x3+…+a10x10都成立，那么（a0+a1）+（a0+a2）+（a0+a3）+…+（a0+a10）=
10
．（用数字作答）分析：将x=0，x=1分别代入等式，当x=0时可以得到a0的值．当x=1时，可以得到a0+a1+a2+…+a9+a10的值，由此可以得到（a0+a1）+（a0+a2）+（a0+a3）+…+（a0+a10）的值．
解答：解：由题意可知：
当x=0时，（1-2x）10=1=a0+a1x+a2x2+a3x3+…+a10x10=a0．
当x=1时，（1-2x）10=1=a0+a1x+a2x2+a3x3+…+a10x10=a0+a1+a2+…+a9+a10．
所以（a0+a1）+（a0+a2）+（a0+a3）+…+（a0+a10）
=a0+a1+a2+…+a9+a10+9a0=1+9=10．
故答案为：10．
当x=0时，（1-2x）10=1=a0+a1x+a2x2+a3x3+…+a10x10=a0．
当x=1时，（1-2x）10=1=a0+a1x+a2x2+a3x3+…+a10x10=a0+a1+a2+…+a9+a10．
所以（a0+a1）+（a0+a2）+（a0+a3）+…+（a0+a10）
=a0+a1+a2+…+a9+a10+9a0=1+9=10．
故答案为：10．
点评：本题考查了等式的应用．从等式分析a0的值和a0+a1+a2+…+a9+a10的值是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
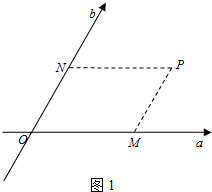如图1，在平面内取一点O，过点O作两条夹角为60°的数轴，使它们以点O为公共原点且具有相同的单位长度，这样在平面内建立的坐标系称为斜坐标系，我们把水平放置的数轴称为横轴（记作a轴），将斜向放置的数轴称为斜轴（记作b轴）．类似
如图1，在平面内取一点O，过点O作两条夹角为60°的数轴，使它们以点O为公共原点且具有相同的单位长度，这样在平面内建立的坐标系称为斜坐标系，我们把水平放置的数轴称为横轴（记作a轴），将斜向放置的数轴称为斜轴（记作b轴）．类似
