题目内容
已知:如图,在平面直角坐标系中,点O为坐标原点以y轴负半轴上一点A为圆心,5为半径作圆A,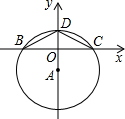 交x轴于点B,点C,交y轴于点D、点E,tan∠DBO=
交x轴于点B,点C,交y轴于点D、点E,tan∠DBO=| 1 | 2 |
求:(1)点D的坐标;
(2)直线CD的函数解析式.
分析:(1)利用∠DAB=2∠DBO以及BA=5可以计算出OA和OD的长度,即可求出D点坐标;
(2)根据(1)中结果可以求出OC长度,即可求出C点坐标,将C和D的坐标代入直线CD中即可求出直线CD的函数解析式.
(2)根据(1)中结果可以求出OC长度,即可求出C点坐标,将C和D的坐标代入直线CD中即可求出直线CD的函数解析式.
解答: 解:如图所示:
解:如图所示:
(1)∵在Rt△BDO中,tan∠DBO=
∴
=
,设DO=a,则BO=2a(1分)
连接AB,∵圆A的半径为5,∴AB=AD=5,AO=5-a(1分)
∵在Rt△ABO中,AO2+BO2=AB2,∴(5-a)2+(2a)2=52(1分)
∴a1=2,a2=0(舍)(1分)
∴D(0,2);(1分)
(2)∵AD⊥BC,∴BO=CO=2a=4(1分)
∴C(4,0)(1分)
设直线CD的函数解析式为y=kx+b(k≠0),把C(4,0),D(0,2)代入,
得
,∴
(2分)
∴直线CD的函数解析式为y=-
x+2.(1分)
 解:如图所示:
解:如图所示:(1)∵在Rt△BDO中,tan∠DBO=
| 1 |
| 2 |
∴
| DO |
| BO |
| 1 |
| 2 |
连接AB,∵圆A的半径为5,∴AB=AD=5,AO=5-a(1分)
∵在Rt△ABO中,AO2+BO2=AB2,∴(5-a)2+(2a)2=52(1分)
∴a1=2,a2=0(舍)(1分)
∴D(0,2);(1分)
(2)∵AD⊥BC,∴BO=CO=2a=4(1分)
∴C(4,0)(1分)
设直线CD的函数解析式为y=kx+b(k≠0),把C(4,0),D(0,2)代入,
得
|
|
∴直线CD的函数解析式为y=-
| 1 |
| 2 |
点评:本题主要考查对于一次函数的综合应用,以及对圆的性质的掌握.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直 如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).
如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).

