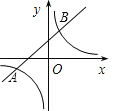
题目内容
【题目】如图,Rt△ABO在直角坐标系中,AB⊥x轴于点B,AO=10,sin∠AOB=![]() ,反比例函数y=
,反比例函数y=![]() (x>0)的图象经过AO的中点C,且与AB交于点D,则BD= .
(x>0)的图象经过AO的中点C,且与AB交于点D,则BD= .
【答案】![]()
【解析】
试题分析:先根据正弦的定义求出AB=6,再利用勾股定理计算出OB=8,则A点坐标为(8,6),由于C点为OA的中点,所以C点坐标为(4,3),根据反比例函数图象上点的坐标特征得到反比例函数解析式为y=![]() ,再确定D点坐标,即可得到BD的长.
,再确定D点坐标,即可得到BD的长.
解:∵AB⊥x轴于点B,
∴∠ABO=90°
∴sin∠AOB=![]() =
=![]() ,而OA=10,
,而OA=10,
∴AB=6,
∴OB=![]() =8,
=8,
∴A点坐标为(8,6),
∵C点为OA的中点,
∴C点坐标为(4,3),
∴k=3×4=12,
∴反比例函数解析式为y=![]() ,
,
把x=8代入得y=![]() =
=![]() ,
,
∴D点坐标为(8,![]() ),
),
∴BD=![]()
故答案为![]() .
.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目