题目内容
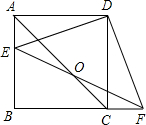
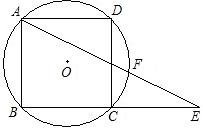已知边长为1的正方形ABCD内接于⊙O，延长BC到点E，使CE=BC，连接AE交⊙O于F，求证：EF，FA的长是方程
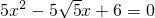的两根．
证明：由勾股定理，得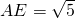
，由割线定理，得EF•AE=EC•EB．
∴
，
，
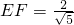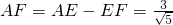将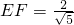代入方程左边=
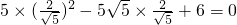，右边=0，
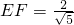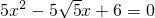∴是方程的根，同理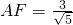
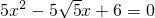也是方程的根，
∴EF、FA是方程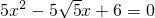的两根．
分析：在直角三角形ABE中，根据勾股定理求得AE的长，再根据割线定理求得EF的长．进一步求得FA的长．然后代入方程进行验证．
点评：熟练运用勾股定理以及割线定理求得线段的长，再进一步验证．
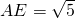，由割线定理，得EF•AE=EC•EB．∴
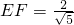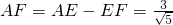，，将
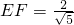代入方程左边=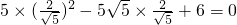，右边=0，∴
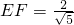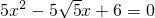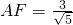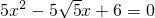是方程的根，同理也是方程的根，∴EF、FA是方程
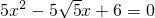的两根．分析：在直角三角形ABE中，根据勾股定理求得AE的长，再根据割线定理求得EF的长．进一步求得FA的长．然后代入方程进行验证．
点评：熟练运用勾股定理以及割线定理求得线段的长，再进一步验证．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
CF．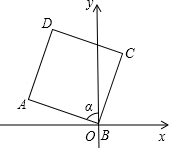
已知边长为1的正方形在坐标系中的位置，如图∠α=75°，求D点的坐标．
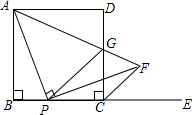如图，已知边长为2的正方形ABCD，P是BC边上一点，E是BC边延长线上一点，过点P作PF⊥AP与∠DCE的平分线CF交于点F．AF与CD交于点G．
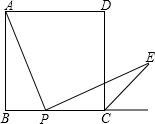（2013•桂林）如图，已知边长为4的正方形ABCD，P是BC边上一动点（与B、C不重合），连结AP，作PE⊥AP交∠BCD的外角平分线于E．设BP=x，△PCE面积为y，则y与x的函数关系式是（ ）
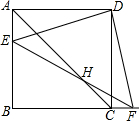如图，已知边长为4的正方形ABCD，点E在AB上，点F在BC的延长线上，EF与AC交于点H，且AE=CF=m，则四边形EBFD的面积为