Question

【题目】某中学开展“数学史”知识竞赛活动，八年级（1）、（2）班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩（满分为100分）如图所示．

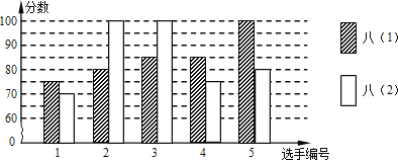
（1）请计算八（1）班、八（2）班两个班选出的5名选手复赛的平均成绩；

（2）请判断哪个班选出的5名选手的复赛成绩比较稳定，并说明理由？

Answer 1

【答案】（1）八（1）班和八（2）班两个班选出的5名选手复赛的平均成绩均为85分；（2）八（1）班的成绩比较稳定，见解析

【解析】

（1）根据算术平均数的概念求解可得；

（2）先计算出两个班的方差，再根据方差的意义求解可得．

（1）=（75+80+85+85+100）=85（分），

=（70+100+100+75+80）=85（分），

所以，八（1）班和八（2）班两个班选出的5名选手复赛的平均成绩均为85分．

（2）八（1）班的成绩比较稳定．

理由如下：

s2八（1）=[（75-85）2+（80-85）2+（85-85）2+（85-85）2+（100-85）2]=70，

s2八（2）=[（70-85）2+（100-85）2+（100-85）2+（75-85）2+（80-85）2]=160，

∵s2八（1）＜s2八（2）

∴八（1）班的成绩比较稳定．