��Ŀ����
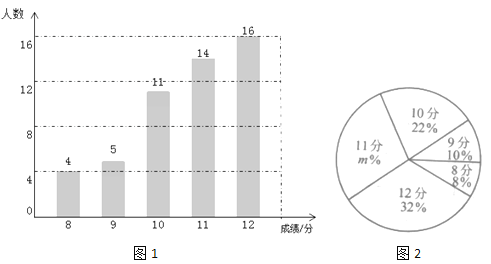
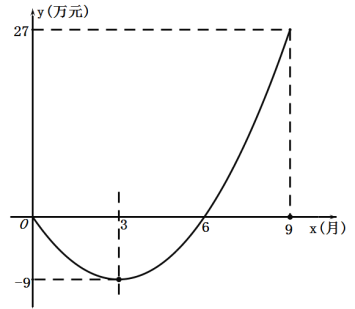
����Ŀ����ѧ��С���ͬѧһ��������ҵ������һ�ҹ�˾����˾�Ծ�Ӫ��ӯ�������ÿ�µ����һ�����һ��.��1��12�·��У��ù�˾ǰx�����ۼƻ�õ�������y����Ԫ��������ʱ��x���£�֮��������κ�����ϵ.
��1����y��x������ϵʽ.
��2���ù�˾���ĸ��¿�ʼ��Ť��Ϊӯ��������ӯ����? ֱ��д��9�·�һ����������õ�����.
��3����ǰ12 �����У��ĸ��¸ù�˾�������������������Ϊ���٣�
���𰸡���1��![]() ����2����4�·���Ť��Ϊӯ�� 9�·�һ��������Ϊ11��Ԫ ����3��12��17��Ԫ.
����2����4�·���Ť��Ϊӯ�� 9�·�һ��������Ϊ11��Ԫ ����3��12��17��Ԫ.
��������
��1����������������ߵĶ�������Ϊ![]() ����������ߵĶ���ʽ����
����������ߵĶ���ʽ����![]() ���뼴�����
���뼴�����![]() ��ֵ����
��ֵ����![]() ��ֵ���������ߵĶ���ʽ�м���ȷ���������ߵĽ���ʽ��
��ֵ���������ߵĶ���ʽ�м���ȷ���������ߵĽ���ʽ��
��2����ͼ�ɽ����8��9�����·ݵ�������IJΪ9�µ�����
��3������ǰ![]() ����������õ������ȥǰ
����������õ������ȥǰ![]() ����������õ������ɱ�ʾ����
����������õ������ɱ�ʾ����![]() ����������õ�����Ϊ����
����������õ�����Ϊ����![]() ��һ�κ�������Ϊ���������õ�
��һ�κ�������Ϊ���������õ�![]() ȡ���Ϊ12ʱ����
ȡ���Ϊ12ʱ����![]() ���뼴�������������
���뼴�������������
��1������������裺![]() ��
��
�ߵ�![]() ���������ϣ�
���������ϣ�
��![]() ��
��
��ã�![]() ��
��
��![]() ��
��![]() ��
��
��2����![]() ���Գ���Ϊֱ��
���Գ���Ϊֱ��![]() ��
��
�൱![]() ʱy��x�����������
ʱy��x�����������
���4�·���Ť��Ϊӯ��
8�·�ǰ��������Ϊ��![]() ��Ԫ,
��Ԫ,
9�·�ǰ��������Ϊ��![]() ��Ԫ,
��Ԫ,
��9�·�һ��������Ϊ��![]() ��Ԫ��
��Ԫ��
��3���赥������ΪW��Ԫ��
������ã�![]() ��
��
�����ã�![]() ��
��
��![]() ��
��
��W��![]() ���������
���������
�൱x��12ʱ����������������Ϊ17��Ԫ