题目内容
如图,点A的坐标为(-2,0),点B的坐标为(8,0),以AB为直径作⊙O/,交 轴的负半轴于点C,则点C的坐标为 ,若二次函数
轴的负半轴于点C,则点C的坐标为 ,若二次函数 的图像经过点A,C,B.已知点P是该抛物线上的动点,当∠APB是锐角时,点P的横坐标
的图像经过点A,C,B.已知点P是该抛物线上的动点,当∠APB是锐角时,点P的横坐标 的取值范围是_____________
的取值范围是_____________
(0,-4), 或
或 或
或
解析试题分析:连接CO/,由点A的坐标与点B的坐标可得圆的直径,即可得到半径,再根据勾股定理即可求得点C的坐标;根据抛物线的对称性,直径所对的圆周角是直角,再根据∠APB是锐角,即可得到结果.
如图,连接CO/,
由题意得AB=10,则AO/=CO/=5,OO/=3 ,
, ,解得
,解得 ,
,
∴点C的坐标为(0,-4), 二次函数
二次函数 的图像经过点A,C,B,
的图像经过点A,C,B,
∴抛物线的对称轴为 ,
,
∴点C关于对称轴 的对称点为(6,-4)
的对称点为(6,-4) 直径所对的圆周角是直角,
直径所对的圆周角是直角,
∴当∠APB是锐角时,点P的横坐标 的取值范围是
的取值范围是 或
或 或
或 .
.
考点:本题考查的是垂径定理,勾股定理,二次函数的性质
点评:解答本题的关键是熟练掌握抛物线的对称性,直径所对的圆周角是直角.

练习册系列答案
相关题目
 (2012•桂平市三模)如图,点P的坐标为(2,
(2012•桂平市三模)如图,点P的坐标为(2, 已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧.
已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧. 如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为
如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为 如图,点A的坐标为( )
如图,点A的坐标为( )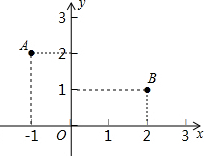 如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )
如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )