题目内容
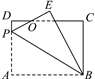
【题目】如图,长方形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,求AP的长.
【答案】AP=4.8.
【解析】
由折叠的性质得出EP=AP,∠E=∠A=90°,BE=AB=8,由ASA证明△ODP≌△OEG,得出OP=OG,PD=GE,设AP=EP=x,则PD=GE=6-x,DG=x,求出CG、BG,根据勾股定理得出方程,解方程即可.
如图所示,设BE与CD交于点G,

∵四边形ABCD是长方形,
∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8.,
根据题意,得△ABP≌△EBP,
∴AP=EP,∠A=∠E=90°,AB=EB=8.
在△ODP和△OEG中,
∵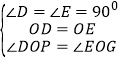 ,
,
∴△ODP≌△OEG,
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=6-x,DG=x,
∴CG=8-x,BG=8-(6-x)=2+x,
根据勾股定理,得BC2+CG2=BG2,
即62+(8-x)2=(2+x)2,
解得x=4.8,
∴AP=4.8.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】如图,数轴上一动点![]() 从原点出发,在数轴上进行往返运动,运动情况如下表(注:表格中的
从原点出发,在数轴上进行往返运动,运动情况如下表(注:表格中的![]() 表示2到4之间的数).
表示2到4之间的数).
![]()
运动次数 | 运动方向 | 运动路程 | 数轴上对应的数 |
第1次 | _________ | 3 | -3 |
第2次 | 左 |
| _________ |
第3次 | _________ | _________ |
|
回答下列问题:
(1)完成表格;
(2)已知第4次运动的路程为![]() .
.
①此时数轴上对应的数是_________;
②若第4次运动后点![]() 恰好回到原点,则这4次运动的总路程是多少?
恰好回到原点,则这4次运动的总路程是多少?



