题目内容
【题目】如图(1),在![]() 中,已知
中,已知![]() ,
,![]() ,把一块含
,把一块含![]() 角的三角板
角的三角板![]() 的直角顶点
的直角顶点![]() 放在
放在![]() 的中点上(直角三角板的短直角边为
的中点上(直角三角板的短直角边为![]() ,长直角边为
,长直角边为![]() ),将直角三角板
),将直角三角板![]() 绕
绕![]() 点按逆时针方向旋转.
点按逆时针方向旋转.
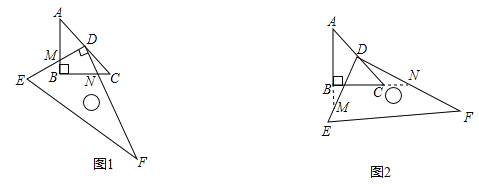
(1)在图(1)中,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() .
.
①证明![]() ;
;
②在这一过程中,直角三角板![]() 与
与![]() 的重叠部分为四边形
的重叠部分为四边形![]() ,请说明四边形
,请说明四边形![]() 的面积是否发生变化?若发生变化,请说明是如何变化的,若不发生变化,求出其面积.
的面积是否发生变化?若发生变化,请说明是如何变化的,若不发生变化,求出其面积.
(2)继续旋转至如图(2)的位置,延长![]() 交
交![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,
,![]() 是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
【答案】(1)①见解析;②四边形![]() 的面积不发生变化.
的面积不发生变化.![]() ;(2)
;(2)![]() 仍然成立.证明见解析;(3)
仍然成立.证明见解析;(3)![]() .
.
【解析】
(1)①连接BD,证明△DMB≌△DNC.根据已知,全等条件已具备两个,再证出∠MDB=∠NDC,用ASA证明全等,
②四边形DMBN的面积不发生变化,因为它的面积始终等于△ABC面积的一半;
(2)成立.同样利用(1)中的证明方法可以证出△DMB≌△DNC;
(1)①如图1,连接DB,在Rt△ABC中,AB=BC,AD=DC,
∴DB=DC=AD,∠BDC=90°,
∴∠ABD=∠C=45°,
∵∠MDB+∠BDN=∠CDN+∠BDN=90°,
∴∠MDB=∠NDC,
∴△BMD≌△CND(ASA),
∴DM=DN;
②四边形DMBN的面积不发生变化;
由①知△BMD≌△CND,
∴S△BMD=S△CND,
∴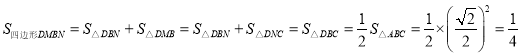 .
.
(2)![]() 仍然成立.证明:
仍然成立.证明:
如图(2),联结![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
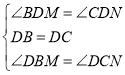 ,
,
∴![]() ≌
≌![]() (ASA).
(ASA).
∴![]() .
.
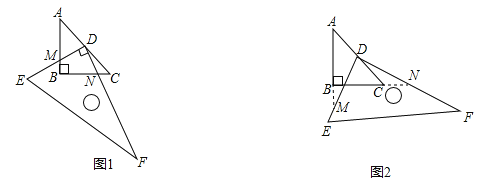

【题目】为了迎接五一黄金周的购物高峰,某品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
运动鞋价格 | 甲 | 乙 |
进价(元/双) | m | m﹣30 |
售价(元/双) | 240 | 160 |
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)若购进乙种运动鞋x(双),要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于13000元且不超过13500元,问该专卖店有几种进货方案;
(3)在(2)的条件下求出总利润y(元)与购进乙种运动鞋x(双)的函数关系式,并用关系式说明哪种方案的利润最大,最大利润是多少.