题目内容
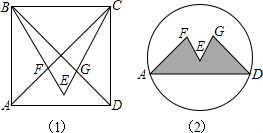
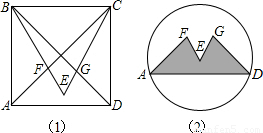
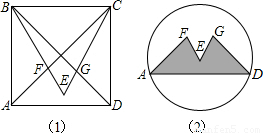
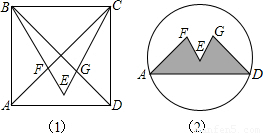
芜湖国际动漫节期间,小明进行了富有创意的形象设计.如图1,他在边长为1的正方形ABCD内作等边三角形BCE,并与正方形的对角线交于F、G点,制成如图2的图标.则图标中阴影部分图形AFEGD的面积= .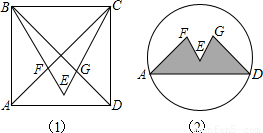
【答案】分析:根据等边三角形与正方形的性质,求出∠EBO,再在直角三角形BOF中利用角的正切求出边OF,从而得知S△BOF,S△BAF=S△BAO-S△BOF;同理求得S△CGD,所以图标中阴影部分图形AFEGD的面积就是:S□ABCD-S△CBE-S△BAF-S△CGD
解答: 解:方法1:设AC与BD交于点O,
解:方法1:设AC与BD交于点O,
∵AC、BD是正方形的对角线,
∴AC⊥BD,OA=OB,
在△BCE中,∠EBC=60°,∠OBC=45°,
∴∠EBO=60°-45°,
∴FO=tan(60°-45°)•OB,
∴S△BOF= OF•OB=
OF•OB= tan(60°-45°)•OB2,
tan(60°-45°)•OB2,
∴S△BAF=S△BAO-S△BOF=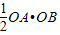 -
- tan(60°-45°)•OB2=
tan(60°-45°)•OB2=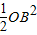 -
- tan(60°-45°)•OB2=
tan(60°-45°)•OB2=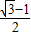 OB2,
OB2,
同理,得S△CGD=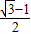 OB2,
OB2,
∵S△CBE=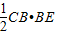 sin60°=
sin60°=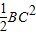 sin60°=
sin60°=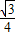 AB2,
AB2,
∴S□ABCD-S△CBE-S△BAF-S△CGD=AB2-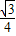 AB2-
AB2- OB2,
OB2,
∵OB= BD,BD2=AB2+AD2,AB=AD=1,
BD,BD2=AB2+AD2,AB=AD=1,
∴S□ABCD-S△CBE-S△BAF-S△CGD=1-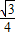 -(
-(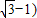 ×
× ×(1+1)=
×(1+1)=
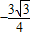 ,
,
图标中阴影部分图形AFEGD的面积=
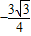 .
.
方法2:过G作GH⊥CD于H,
则易得△GDH是等腰直角三角形,设DH=GH=x,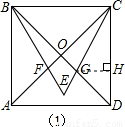
∵△BEC是等边三角形,
∴∠BCE=60°,
∴∠ECD=90°-60°=30°,
∴CH= x,
x,
∵CD=DH+CH=1,
即x+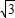 x=1,
x=1,
x(1+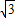 )=1,
)=1,
解得x=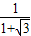 =
=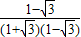 =
=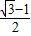 ,
,
∴S△CGD= ×1×
×1×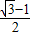 =
=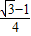
同理S△BFA=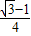
易得S△BCE=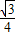
∴S阴影=S正方形ABCD-S△BCE-S△BAF-S△CGD
=1-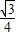 -
-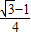 -
-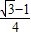
=
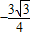 .
.
故答案为:
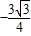 .
.
点评:解答本题的难点是求直角三角形ABO中的三角形ABF的面积,在突破难点时,充分利用了等边三角形、正方形的性质以及直角三角形中的边角函数关系.
解答:
 解:方法1:设AC与BD交于点O,
解:方法1:设AC与BD交于点O,∵AC、BD是正方形的对角线,
∴AC⊥BD,OA=OB,
在△BCE中,∠EBC=60°,∠OBC=45°,
∴∠EBO=60°-45°,
∴FO=tan(60°-45°)•OB,
∴S△BOF=
 OF•OB=
OF•OB= tan(60°-45°)•OB2,
tan(60°-45°)•OB2,∴S△BAF=S△BAO-S△BOF=
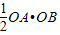 -
- tan(60°-45°)•OB2=
tan(60°-45°)•OB2=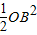 -
- tan(60°-45°)•OB2=
tan(60°-45°)•OB2=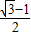 OB2,
OB2,同理,得S△CGD=
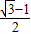 OB2,
OB2,∵S△CBE=
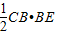 sin60°=
sin60°=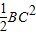 sin60°=
sin60°=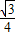 AB2,
AB2,∴S□ABCD-S△CBE-S△BAF-S△CGD=AB2-
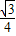 AB2-
AB2- OB2,
OB2,∵OB=
 BD,BD2=AB2+AD2,AB=AD=1,
BD,BD2=AB2+AD2,AB=AD=1,∴S□ABCD-S△CBE-S△BAF-S△CGD=1-
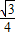 -(
-(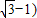 ×
× ×(1+1)=
×(1+1)=
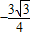 ,
,图标中阴影部分图形AFEGD的面积=

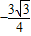 .
.方法2:过G作GH⊥CD于H,
则易得△GDH是等腰直角三角形,设DH=GH=x,

∵△BEC是等边三角形,
∴∠BCE=60°,
∴∠ECD=90°-60°=30°,
∴CH=
 x,
x,∵CD=DH+CH=1,
即x+
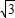 x=1,
x=1,x(1+
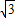 )=1,
)=1,解得x=
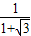 =
=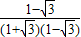 =
=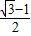 ,
,∴S△CGD=
 ×1×
×1×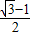 =
=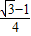
同理S△BFA=
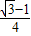
易得S△BCE=
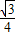
∴S阴影=S正方形ABCD-S△BCE-S△BAF-S△CGD
=1-
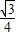 -
-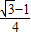 -
-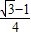
=

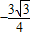 .
.故答案为:

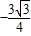 .
.点评:解答本题的难点是求直角三角形ABO中的三角形ABF的面积,在突破难点时,充分利用了等边三角形、正方形的性质以及直角三角形中的边角函数关系.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
芜湖国际动漫节期间,小明进行了富有创意的形象设计.如图1,他在边长为1的正方形ABCD内作等边三角形BCE,并与正方形的对角线交于F、G点,制成如图2的图标.则图标中阴影部分图形AFEGD的面积= .